题目内容
7.函数f(x)=x•2|x|-x-2的零点个数为( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 转化函数为方程,通过两个函数的图象交点个数判断求解即可.
解答 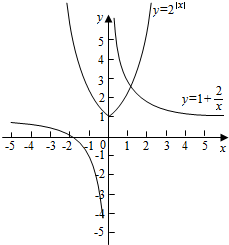 解:函数f(x)=x•2|x|-x-2的零点,
解:函数f(x)=x•2|x|-x-2的零点,
转化为方程x•2|x|=x+2的根的个数,
即2|x|=1+$\frac{2}{x}$,作出两个函数的图象y=2|x|,y=1+$\frac{2}{x}$,
如图:两个函数的图象有一个交点.
故选:C.
点评 本题考查函数的零点的求法,零点个数问题,考查数形结合以及计算能力,转化思想的应用.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
18.已知集合A={x|$\frac{6}{x+1}$≥1},B={x|x2>1},则集合M={x|x∈A且x∉B}=( )
| A. | (-1,1] | B. | [-1,1] | C. | (1,5] | D. | [1,5] |
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1、F2,过F1作圆x2+y2=a2的切线分别交双曲线的左、右两支于点B、C,且|BC|=|CF2|,则双曲线的渐近线方程为( )
| A. | y=±3x | B. | y=±2$\sqrt{2}$x | C. | y=±($\sqrt{3}$+1)x | D. | y=±($\sqrt{3}$-1)x |
19.将y=2cos($\frac{x}{3}$+$\frac{π}{6}$)图象按向量$\overrightarrow{a}$=(-$\frac{π}{4}$,-2)平移,则平移后所得函数的周期及图象的一个对称中心分别为( )
| A. | 3π,$({\frac{π}{4},-2})$ | B. | 6π,$({\frac{3π}{4},2})$ | C. | 6π,$({\frac{3π}{4},-2})$ | D. | 3π,$({\frac{π}{4},2})$ |
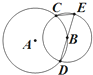 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4. 如图所示:在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,O,Q分别为AB,PA的中点,G为△AOC的重心,AC=$\sqrt{3}$,∠ABC=30°
如图所示:在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,O,Q分别为AB,PA的中点,G为△AOC的重心,AC=$\sqrt{3}$,∠ABC=30° 如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.
如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.