题目内容
8.已知函数f(x)=x-ln(x+a)的最小值为0,其中a>0.(Ⅰ)求a的值;
(Ⅱ)已知结论:若函数f(x)=x-ln(x+a)在区间(m,n)内导数都存在,且m>-a,则存在x0∈(m,n),使得$f'({x_0})=\frac{f(n)-f(m)}{n-m}$.试用这个结论证明:若-a<x1<x2,设函数$g(x)=\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}(x-{x_1})+f({x_1})$,则对任意x∈(x1,x2),都有f(x)<g(x);
(Ⅲ)若et+n≥1+n对任意的正整数n都成立(其中e为自然对数的底),求实数t的最小值.
分析 (Ⅰ)求函数的导数,利用函数的最值建立方程关系即可求a的值;
(Ⅱ)根据所给的结论,将条件进行转化进行证明即可.
(Ⅲ)利用取对数法将不等式进行转化,结合(Ⅰ)的结论,求对应式子的最值即可.
解答 解:(Ⅰ)函数的定义域为(-a,+∞),
函数的f(x)的导数f′(x)=1-$\frac{1}{x+a}$=$\frac{x+a-1}{x+a}$,
由f′(x)=0得,x=1-a>-a,
即由f′(x)>0得x>1-a,
由f′(x)<0得-a<x<1-a,
即当x=1-a时,函数f(x)取得极小值同时也是最小值f(1-a)=1-a=0,
解得a=1;
(Ⅱ)令h(x)=f(x)-g(x)=f(x)-$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$(x-x1)-f(x1);
则h′(x)=f′(x)-$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$,
∵f(x)在x∈(x1,x2),上存在导数,
∴存在x0∈(x1,x2),使得f′(x0)=$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$,
∵f′(x)=$\frac{x}{1+x}$,
∴h′(x)=f′(x)-f′(x0)=$\frac{x}{1+x}$-$\frac{{x}_{0}}{1+{x}_{0}}$=$\frac{x-{x}_{0}}{(1+x)(1+{x}_{0})}$,
当x∈(x1,x0),h′(x)<0,
∴h(x)为单调减函数,∴h(x)<h(x1)=0,
当x∈(x0,x2),h′(x)>0,
∴h(x)为单调增函数,∴h(x)<h(x2)=0,
故对任意x∈(x1,x2),都有f(x)<g(x);
(Ⅲ)由et+n≥1+n两边取对数得t+n≥ln(1+n),
故t≥-n+ln(1+n),
由(Ⅰ)知,f(x)=x-ln(x+1)在[-1,+∞)上单调递增,
故-x+ln(1+x)在[-1,+∞)上单调递减,
∵n是正整数,
∴当n=1时,-n+ln(1+n)的最大值为-1+ln2,
∴若t≥-n+ln(1+n)恒成立,
则t的最小值为-1+ln2.
点评 本题主要考查导数的综合应用,函数的最值,极值,单调性和导数之间的关系,考查学生的运算能力,综合性较强,运算量较大,有一定的难度.

| A. | (-1,1] | B. | [-1,1] | C. | (1,5] | D. | [1,5] |
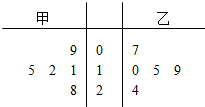 某区今年春季运动会共有5场篮球比赛,其中甲、乙两运动员得分的茎叶图如图所示.
某区今年春季运动会共有5场篮球比赛,其中甲、乙两运动员得分的茎叶图如图所示.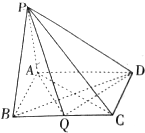 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).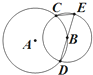 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.