题目内容
2．用反证法证明：$\sqrt{2}，\sqrt{3}，\sqrt{5}$不可能成等差数列．分析 假设$\sqrt{2}，\sqrt{3}，\sqrt{5}$这三个数成等差数列，则由等差数列的性质可得2$\sqrt{3}$=$\sqrt{2}$+$\sqrt{5}$，能推出64=55 （矛盾 ）．
解答 证明：假设$\sqrt{2}，\sqrt{3}，\sqrt{5}$这三个数成等差数列，则由等差数列的性质可得2$\sqrt{3}$=$\sqrt{2}$+$\sqrt{5}$，
∴12=2+5+2$\sqrt{10}$，∴5=2$\sqrt{10}$，∴25=40（矛盾），故假设不成立，
∴$\sqrt{2}，\sqrt{3}，\sqrt{5}$这三个数不可能成等差数列．
点评 本题考查用反证法证明不等式，用反证法证明不等式的关键是推出矛盾．
练习册系列答案
相关题目
12．某天连续有7节课，其中语文、英语、物理、化学、生物5科各1节，数学2节．在排课时，要求生物课不排第1节，数学课要相邻，英语课与数学课不相邻，则不同排法的种数是（ ）
| A． | 408 | B． | 480 | C． | 552 | D． | 816 |
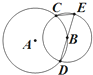如图，圆A与圆B交于C、D两点，圆心B在圆A上，DE为圆B的直径，已知CE=1，DE=4，则圆A的半径为4．
11．二项式$（\frac{1}{{\sqrt{x}}}-{x^2}{）^{10}}$的展开式中的常数项是（ ）
| A． | -45 | B． | -10 | C． | 45 | D． | 65 |
如图所示：在三棱锥P-ABC中，PA⊥底面ABC，AC⊥BC，O，Q分别为AB，PA的中点，G为△AOC的重心，AC=$\sqrt{3}$，∠ABC=30°