题目内容
6.已知向量$\overrightarrow a=(cosθ,sinθ)$,向量$\overrightarrow b=(\sqrt{3},-1)$,则|2$\overrightarrow a-\overrightarrow b|$的最大值,最小值分别是( )| A. | 4,0 | B. | $4\sqrt{2}$,4 | C. | $4\sqrt{2}$,0 | D. | 16,0 |
分析 利用向量的坐标运算得到|2$\overrightarrow a-\overrightarrow b|$用θ的三角函数表示化简求最值.
解答 解:向量$\overrightarrow a=(cosθ,sinθ)$,向量$\overrightarrow b=(\sqrt{3},-1)$,则2$\overrightarrow{a}-\overrightarrow{b}$=(2cosθ-$\sqrt{3}$,2sinθ+1),
所以|2$\overrightarrow a-\overrightarrow b|$2=(2cosθ-$\sqrt{3}$)2+(2sinθ+1)2=8-4$\sqrt{3}$cosθ+4sinθ=8-8sin($θ-\frac{π}{3}$),
所以|2$\overrightarrow a-\overrightarrow b|$2的最大值,最小值分别是:16,0;
所以|2$\overrightarrow a-\overrightarrow b|$的最大值,最小值分别是4,0;
故选:A.
点评 本题考查了向量的坐标运算以及三角函数解析式的化简;利用了两角差的正弦公式以及正弦函数的有界性.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
1.复数$\frac{3+i}{1-3i}$+$\frac{1}{i}$等于( )
| A. | 3-i | B. | -2i | C. | 2i | D. | 0 |
11.二项式$(\frac{1}{{\sqrt{x}}}-{x^2}{)^{10}}$的展开式中的常数项是( )
| A. | -45 | B. | -10 | C. | 45 | D. | 65 |
18.已知集合A={x|$\frac{6}{x+1}$≥1},B={x|x2>1},则集合M={x|x∈A且x∉B}=( )
| A. | (-1,1] | B. | [-1,1] | C. | (1,5] | D. | [1,5] |
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1、F2,过F1作圆x2+y2=a2的切线分别交双曲线的左、右两支于点B、C,且|BC|=|CF2|,则双曲线的渐近线方程为( )
| A. | y=±3x | B. | y=±2$\sqrt{2}$x | C. | y=±($\sqrt{3}$+1)x | D. | y=±($\sqrt{3}$-1)x |
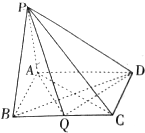 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).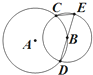 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4. 如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.
如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.