题目内容
9.若$\frac{1}{27}$≤x≤9,则f(x)=log3$\frac{x}{27}$•log3(3x)( )| A. | 有最小值-$\frac{32}{9}$,最大值-3 | B. | 有最小-4,最大值12 | ||
| C. | 有最小值-$\frac{32}{9}$,无最大值 | D. | 无最小值,有最大值12 |
分析 化简函数的解析式,通过x的范围,求解函数的最值即可.
解答 解:f(x)=log3$\frac{x}{27}$•log3(3x)=(log3x-3)(1+log3x)=log23x-2log3x-3,令log3x=t,
∵$\frac{1}{27}$≤x≤9,∴t∈[-3,2].
y=t2-2t-3=(t-1)2-4,t=1时,函数取得最小值:-4,t=-3时函数取得最大值12.
故选:B.
点评 本题考查函数的最值,二次函数闭区间上的最值的求法,对数的运算法则的应用,考查计算能力.

练习册系列答案
相关题目
1.复数$\frac{3+i}{1-3i}$+$\frac{1}{i}$等于( )
| A. | 3-i | B. | -2i | C. | 2i | D. | 0 |
18.已知集合A={x|$\frac{6}{x+1}$≥1},B={x|x2>1},则集合M={x|x∈A且x∉B}=( )
| A. | (-1,1] | B. | [-1,1] | C. | (1,5] | D. | [1,5] |
19.将y=2cos($\frac{x}{3}$+$\frac{π}{6}$)图象按向量$\overrightarrow{a}$=(-$\frac{π}{4}$,-2)平移,则平移后所得函数的周期及图象的一个对称中心分别为( )
| A. | 3π,$({\frac{π}{4},-2})$ | B. | 6π,$({\frac{3π}{4},2})$ | C. | 6π,$({\frac{3π}{4},-2})$ | D. | 3π,$({\frac{π}{4},2})$ |
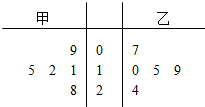 某区今年春季运动会共有5场篮球比赛,其中甲、乙两运动员得分的茎叶图如图所示.
某区今年春季运动会共有5场篮球比赛,其中甲、乙两运动员得分的茎叶图如图所示.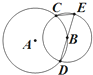 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径,已知CE=1,DE=4,则圆A的半径为4.