题目内容
【题目】己知椭圆
上任意一点到其两个焦点
，
的距离之和等于
，焦距为2c，圆
，
，
是椭圆的左、右顶点，AB是圆O的任意一条直径，四边形
面积的最大值为．
（1）求椭圆C的方程；
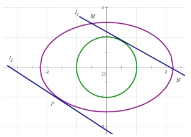
（2）如图，若直线
与圆O相切，且与椭圆相交于M，N两点，直线
与
平行且与椭圆相切于P（O，P两点位于的同侧），求直线，距离d的取值范围．
【答案】（1）
（2）
【解析】
（1）由椭圆的定义知：
，由当直径
轴时四边形
的面积最大，最大为
，可得
，即椭圆方程得解；
（2）由直线
与圆O相切，可得
，
由椭圆与直线相切可得：
，
由两平行线的距离公式可得
，
又
，则可得
，代入运算即可得解.
解：（1）由椭圆的定义知：，
又当直径轴时四边形的面积最大，最大为
，
椭圆
（2）因为直线与圆O相切，
又设直线
，联立
消去y有
化简有
因为，
又
，又
，
，
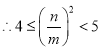
又由O，P两点位于
的同侧，m，n异号，
.
练习册系列答案
相关题目
