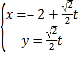题目内容
【题目】在
中，已知
，
，
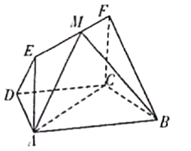
，D是边AC上一点，将
沿BD折起，得到三棱锥
．若该三棱锥的顶点A在底面BCD的射影M在线段BC上，设
，则x的取值范围为（ ）
A.
B.
C.
D.
【答案】B
【解析】
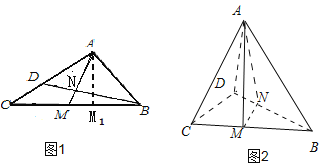
在折叠前图1中，
，垂足为
，设图1中
在线段
上的射影为
，当运动点
与点
无限接近时，折痕
接近，此时与点
无限接近，得到
，在图2中，根据直角三角形的斜边大于直角边，得到
，即可求解．
由将
沿BD折起，得到三棱锥
，且在底面
的射影在线段上，
如图2所示，
平面，则，
在折叠前图1中，作，垂足为，
在图1中过作
于点，当运动点与点无限接近时，折痕接近，此时与点无限接近，
在图2中，由于
是直角
的斜边，
为直角边，所以，
由此可得
,
因为
中，
，
由余弦定理可得
,所以
，
所以
由于
，所以实数
的取值范围是
，
故选B．
练习册系列答案
备战中考寒假系列答案
相关题目
【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如下表所示．
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| n | 0.350 |
第3组 |
| 30 | p |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
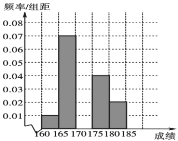
（1）求频率分布表中n，p
（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试，则第3、4、5组每组各抽取多少名学生进入第二轮面试？
（3）在（2）的前提下，学校决定从6名学生中随机抽取2名学生接受甲考官的面试，求第4组至少有1名学生被甲考官面试的概率．
