题目内容
3.设x,y为实数,若4x2+y2=1,则x+y的最大值是$\frac{\sqrt{5}}{2}$.分析 由题意,可令2x=cosα,y=sinα,α∈[-$\frac{π}{2}$,$\frac{π}{2}$],运用两角和的正弦公式,结合正弦函数的值域即可得到最大值.
解答 解:x,y为实数,若4x2+y2=1,
则可令2x=cosα,y=sinα,α∈[-$\frac{π}{2}$,$\frac{π}{2}$],
即有x+y=$\frac{1}{2}$cosα+sinα=$\frac{\sqrt{5}}{2}$($\frac{\sqrt{5}}{5}$cosα+$\frac{2\sqrt{5}}{5}$sinα)
=$\frac{\sqrt{5}}{2}$sin(α+θ)(θ为第一象限角,tanθ=$\frac{1}{2}$),
当α+θ=2kπ+$\frac{π}{2}$,k∈Z时,sin(α+θ)取得最大值1,
则有x+y的最大值为$\frac{\sqrt{5}}{2}$.
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查椭圆参数方程的运用,考查三角函数的化简和求值,属于中档题.

练习册系列答案
相关题目
16.已知α∈(π,2π),且cosα+sinα=$\frac{1}{5}$,则tanα=( )
| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
14.已知命题p:若a>b,则a2>b2;q:“x≤1”是“x2+2x-3≤0”的必要不充分条件.则下列命题是真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | ¬p∧¬q | D. | p∧¬q |
15.已知一几何体的三视图如图所示,则该几何体的体积是( )
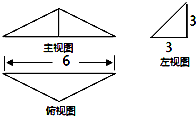

| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
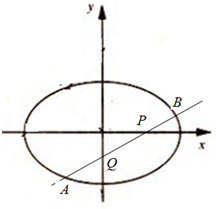 已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.
已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.