Question

11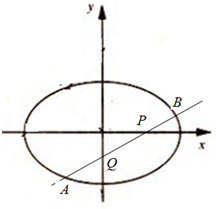．已知椭圆$\frac{{x}^{2}}{2}$+y²=1，过点P（1，0）作直线l，使l交椭圆于A，B两点，且交y轴于Q点，若|AQ|=|BP|．求直线l的方程．

Answer 1

分析 设出直线方程，利用已知条件转化为PQ的中点与AB的中点重合，求解直线的斜率，即可得到直线方程．

解答 解：设直线l方程为：y=k（x-1），椭圆$\frac{{x}^{2}}{2}$+y²=1，过点P（1，0）作直线l，使l交椭圆于A，B两点，且交y轴于Q点，若|AQ|=|BP|．可知PQ的中点与AB的中点重合，Q（0，-K），PQ的中点（$\frac{1}{2}$，-$\frac{k}{2}$），
由$\left\{\begin{array}{l}\frac{{x}^{2}}{2}+{y}^{2}=1\\ y=k（x-1）\end{array}\right.$，可得$\frac{{x}^{2}}{2}$+k²（x-1）²=1，
可得：（1+2k²）x²-4k²x+2k²-2=0，设A（x₁，y₁），B（x₂，y₂），
则x₁+x₂=$\frac{4{k}^{2}}{1+2{k}^{2}}$，
由题意可得$\frac{4{k}^{2}}{1+2{k}^{2}}=1$，解得k=$±\frac{\sqrt{2}}{2}$，
直线l的方程：y=$\frac{\sqrt{2}}{2}$x-$\frac{\sqrt{2}}{2}$，或y=-$\frac{\sqrt{2}}{2}x$$+\frac{\sqrt{2}}{2}$．

点评 本题考查直线与椭圆方程的综合应用，考查转化思想的应用，分析问题解决问题的能力以及计算能力．