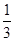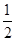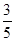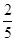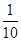题目内容
已知圆C:x2+y2=12,直线l:4x+3y=25,则圆C上任意一点A到直线l的距离小于2的概率为________.
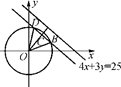

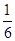
由点到直线的距离公式可得圆心到直线l的距离为d=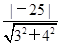 =5,当圆C上的点到直线l的距离是2时有两个点为点B与点D,设过这两点的直线方程为4x+3y+c=0,得c=15,要使圆上点到直线的距离小于2,即l1:4x+3y=15与圆相交所得劣弧上,由圆的半径为2
=5,当圆C上的点到直线l的距离是2时有两个点为点B与点D,设过这两点的直线方程为4x+3y+c=0,得c=15,要使圆上点到直线的距离小于2,即l1:4x+3y=15与圆相交所得劣弧上,由圆的半径为2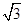 ,圆心到直线的距离为3可知劣弧所对圆心角为
,圆心到直线的距离为3可知劣弧所对圆心角为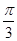 ,故所求概率为P=
,故所求概率为P=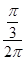 =
=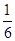 .
.
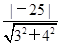 =5,当圆C上的点到直线l的距离是2时有两个点为点B与点D,设过这两点的直线方程为4x+3y+c=0,得c=15,要使圆上点到直线的距离小于2,即l1:4x+3y=15与圆相交所得劣弧上,由圆的半径为2
=5,当圆C上的点到直线l的距离是2时有两个点为点B与点D,设过这两点的直线方程为4x+3y+c=0,得c=15,要使圆上点到直线的距离小于2,即l1:4x+3y=15与圆相交所得劣弧上,由圆的半径为2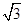 ,圆心到直线的距离为3可知劣弧所对圆心角为
,圆心到直线的距离为3可知劣弧所对圆心角为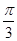 ,故所求概率为P=
,故所求概率为P=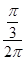 =
=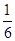 .
.
练习册系列答案
相关题目
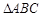 的三顶点坐标为
的三顶点坐标为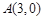 ,
,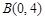 ,
,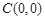 ,
,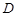 点的坐标为
点的坐标为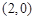 ,向
,向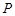 ,那么点
,那么点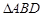 内的概率为( ).
内的概率为( ).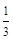
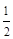
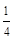
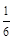
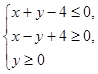 表示的平面区域为M,不等式组
表示的平面区域为M,不等式组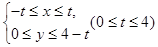 表示的平面区域为N.在M内随机取一个点,这个点在N内的概率为P.①当
表示的平面区域为N.在M内随机取一个点,这个点在N内的概率为P.①当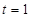 时,P=__________;② P的最大值是_________.
时,P=__________;② P的最大值是_________.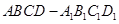 中,
中,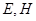 分别是棱
分别是棱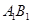 ,
,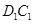 上的点(点
上的点(点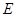 与
与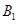 不重合),且
不重合),且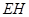 ∥
∥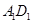 ,过
,过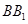 ,
,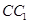 相交,交点分别为
相交,交点分别为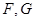 .设
.设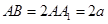 ,
,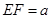 ,
,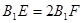 .在长方体
.在长方体 内的概率为 .
内的概率为 .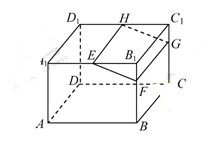
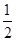 ,则
,则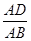 =________.
=________.