��Ŀ����
4��4��23���ǡ���������ա���ij��ѧ�ڴ��ڼ俪չ��һϵ�еĶ���������Ϊ�˽ⱾУѧ�������Ķ������ѧУ�����ȡ��100��ѧ����������Ķ�ʱ����е��飬�����Ǹ��ݵ��������Ƶ�ѧ���վ������Ķ�ʱ�䣨��λ�����ӣ���Ƶ�ʷֲ�ֱ��ͼ�������վ������Ķ�ʱ�䲻����60���ӵ�ѧ����Ϊ�������ա�������60���ӵ�ѧ����Ϊ���Ƕ����ա�
��1��������֪�����������2��2�������������ݴ��ж��Ƿ���99%�İ�����Ϊ�������ա����Ա��йأ�
| �Ƕ����� | ������ | �ϼ� | |
| �� | 15 | ||
| Ů | 45 | ||
| �ϼ� |
����K2=$\frac{n��ad-bc��^{2}}{��a+b����c+d����a+c����b+d��}$n=a+b+c+d
| P��K2��k0�� | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
���� ��1������Ƶ�ʷֲ�ֱ��ͼ��ֱ�Ӽ�����д����Ȼ�����ø������K2���жϼ��ɣ�
��2��������ʵķֲ��У�Ȼ�����ó����ηֲ���������뷽��ɣ�
��� �⣺��1����������2��2����������
| �Ƕ����� | ������ | �ϼ� | |
| �� | 40 | 15 | 55 |
| Ů | 20 | 25 | 45 |
| �ϼ� | 60 | 40 | 100 |
${K}^{2}=\frac{100{��40��25-15��20��}^{2}}{60��40��55��45}$��8.249
VB8.249��6.635������99%�İ�����Ϊ�������ԡ����Ա��йء���6�֣�
��2����Ƶ��Ϊ���ʣ���Ӹ�Уѧ���������ȡ1��ѧ��ǡΪ�����Եĸ���Ϊ$\frac{2}{5}$���������֪X��B��3��$\frac{2}{5}$����P��x=i��=${C}_{3}^{i}��\frac{2}{5}��^{i}��\frac{3}{5}��^{3-i}$ ��i=0��1��2��3������8�֣�
�Ӷ��ֲ���Ϊ
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{125}$ | $\frac{54}{125}$ | $\frac{36}{125}$ | $\frac{8}{125}$ |
E��x��=np=$\frac{6}{5}$��D��x��=np��1-p��=$\frac{18}{25}$ ����12�֣�
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã����������Լ�����ֲ��������뷽������ֲ��е����������������

��ϰ��ϵ�д�
�����Ŀ
14����a=sin145�㣬b=cos52�㣬c=tan47�㣬��a��b��c�Ĵ�С��ϵ�ǣ�������
| A�� | a��b��c | B�� | c��b��a | C�� | b��a��c | D�� | a��c��b |
15��һ����4S���½�A��B��C����γ���ÿ��γ����������±���
ͬһ��γ���ȫ��ͬ��������ȡһ���ֳ�ȥ�μӳ�չ��
���ӵ���һ�������ȡ2����������ȡ��������Ϊͬһ���ͳ��ĸ��ʣ�
������һ������ȡ4����������A��B��C�����ͺŵij������ֱ��Ϊa��b��c���Ǧ�Ϊa��b��c�����ֵ����εķֲ��к���ѧ������
| ��� | A | B | C |
| ���� | 4 | 3 | 2 |
���ӵ���һ�������ȡ2����������ȡ��������Ϊͬһ���ͳ��ĸ��ʣ�
������һ������ȡ4����������A��B��C�����ͺŵij������ֱ��Ϊa��b��c���Ǧ�Ϊa��b��c�����ֵ����εķֲ��к���ѧ������
12����֪�ȱ�����{an}��ǰn���ΪSn����$\frac{S_4}{a_4}=\frac{S_2}{a_2}$����$\frac{{{S_{2015}}}}{S_1}$���ڣ�������
| A�� | 2015 | B�� | -2015 | C�� | 1 | D�� | -1 |
9������{an}Ϊ�Ȳ����У���a1+a7+a13=4����a2+a12��ֵΪ��������
| A�� | $\frac{4}{3}$ | B�� | $\frac{8}{3}$ | C�� | 2 | D�� | 4 |
13��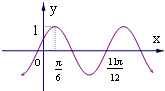 ����f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x����ͼ������ƽ��$\frac{��}{3}$����λ�õ���ͼ�����ʽΪ��������
����f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x����ͼ������ƽ��$\frac{��}{3}$����λ�õ���ͼ�����ʽΪ��������
 ����f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x����ͼ������ƽ��$\frac{��}{3}$����λ�õ���ͼ�����ʽΪ��������
����f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x����ͼ������ƽ��$\frac{��}{3}$����λ�õ���ͼ�����ʽΪ��������| A�� | y=sin��2x-$\frac{��}{6}$�� | B�� | y=cos2x | C�� | y=sin��2x+$\frac{5��}{6}$�� | D�� | y=-cos2x |
 ��ͼ����������ABCDEF�У�AB��CD��EF��CD=EF=CF=2AB=2AD=2����DCF=60�㣬AD��CD��ƽ��CDEF��ƽ��ABCD��
��ͼ����������ABCDEF�У�AB��CD��EF��CD=EF=CF=2AB=2AD=2����DCF=60�㣬AD��CD��ƽ��CDEF��ƽ��ABCD�� ��֪PA��ƽ��ABCD��CD��AD��BA��AD��CD=AD=AP=4��AB=2��
��֪PA��ƽ��ABCD��CD��AD��BA��AD��CD=AD=AP=4��AB=2��