题目内容
12.已知等比数列{an}的前n项和为Sn,若$\frac{S_4}{a_4}=\frac{S_2}{a_2}$,则$\frac{{{S_{2015}}}}{S_1}$等于( )| A. | 2015 | B. | -2015 | C. | 1 | D. | -1 |
分析 由题意和求和公式可得q的方程,解方程可得q,可得S2015,进而可得比值.
解答 解:由题意可得等比数列{an}的公比q≠1,
∵$\frac{S_4}{a_4}=\frac{S_2}{a_2}$,∴S4a2=S2a4,
∴$\frac{{a}_{1}(1-{q}^{4})}{1-q}$•a1q=$\frac{{a}_{1}(1-{q}^{2})}{1-q}$•a1q3,
化简并解方程可得q=-1,
∴S2015=$\frac{{a}_{1}[1-(-1)^{2015}]}{1-(-1)}$=a1,
∴$\frac{{{S_{2015}}}}{S_1}$=$\frac{{a}_{1}}{{a}_{1}}$=1
故选:C.
点评 本题考查等比数列的性质和求和公式,求出数列的公比是解决问题的关键,属基础题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
20.一几何体的三视图如图所示,则该几何体的体积为( )


| A. | $4-\frac{π}{3}$ | B. | $\frac{8}{3}$ | C. | 4-π | D. | $12-2\sqrt{2}π$ |
4.4月23人是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”

(1)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
(2)将频率视为概率,现在从该校大量学生中,用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中的“读书谜”的人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方程D(X)
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$n=a+b+c+d

(1)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
| 非读书迷 | 读书迷 | 合计 | |
| 男 | 15 | ||
| 女 | 45 | ||
| 合计 |
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$n=a+b+c+d
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
2.把函数f(x)=sin(2x+ϕ)$(|ϕ|<\frac{π}{2})$的图象向左平移$\frac{π}{6}$个单位,得到函数g(x)的图象,若g(x)的图象关于$(-\frac{π}{3},0)$对称,则$f(-\frac{π}{2})$=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
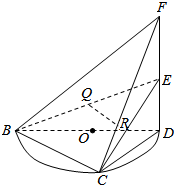 如图:$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,$BF=2\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.
如图:$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,$BF=2\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.