题目内容
16. 已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=2.
已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=2.(1)求证:CD⊥平面ADP;
(2)若M为线段PC上的点,当BM⊥PC时,求三棱锥B-APM的体积.
分析 (1)利用平面与平面垂直的判定定理证明平面ADP⊥平面ABCD,然后利用性质定理证明CD⊥平面ADP.
(2)取CD的中点F,连接BF,求得BP,所以BC=BP.在平面PCD中过点M作MQ∥DC交DP于Q,连接QB,QA,
利用等体积法转化求解即可.
解答  (1)证明:因为PA⊥平面ABCD,PA?平面ADP,
(1)证明:因为PA⊥平面ABCD,PA?平面ADP,
所以平面ADP⊥平面ABCD.…(2分)
又因为平面ADP∩平面ABCD=AD,CD⊥AD,
所以CD⊥平面ADP.…(4分)
(2)取CD的中点F,连接BF,
在梯形ABCD中,因为CD=4,AB=2,
所以BF⊥CD.
又BF=AD=4,所以BC=$2\sqrt{5}$.
在△ABP中,由勾股定理求得BP=$2\sqrt{5}$.
所以BC=BP.…(7分)
又知点M在线段PC上,且BM⊥PC,
所以点M为PC的中点.…(9分)
在平面PCD中过点M作MQ∥DC交DP于Q,连接QB,QA,
则V三棱锥B-APM=V三棱锥M-APB=V三棱锥Q-APM=V三棱锥B-APQ=$\frac{1}{3}×(\frac{1}{2}×4×2)×2$=$\frac{8}{3}$…(12分)
点评 本题考查平面与平面垂直的判定定理以及性质定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力转化思想的应用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
4.4月23人是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”

(1)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
(2)将频率视为概率,现在从该校大量学生中,用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中的“读书谜”的人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方程D(X)
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$n=a+b+c+d

(1)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
| 非读书迷 | 读书迷 | 合计 | |
| 男 | 15 | ||
| 女 | 45 | ||
| 合计 |
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$n=a+b+c+d
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
11.在平面直角坐标系中,角α的顶点与原点重合,始边与x轴的非负半轴重合,终边过点P(-$\sqrt{3}$,-1),则sin(2α-$\frac{π}{2}$)=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |

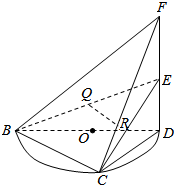 如图:$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,$BF=2\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.
如图:$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,$BF=2\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.