题目内容
8.如图1,直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=2AB=4,BC=2.AE∥BC交CD于点E,点G,H分别在线段DA,DE上,且GH∥AE.将图1中的△AED沿AE翻折,使平面ADE⊥平面ABCE(如图2所示),连结BD、CD,AC、BE.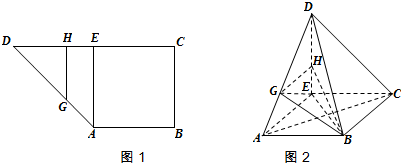
(Ⅰ)求证:平面DAC⊥平面DEB;
(Ⅱ)当三棱锥B-GHE的体积最大时,求直线BG与平面BCD所成角的正弦值.
分析 (Ⅰ)根据折叠前后的边角关系可知道DE⊥底面ABCE,底面ABCE为正方形,从而得到AC⊥DE,AC⊥BE,根据线面垂直的判定定理即可得到AC⊥DBE,再根据面面垂直的判定定理得出平面DAC⊥平面DEB;
(Ⅱ)根据已知条件知道三直线EA,EC,ED两两垂直,从而分别以这三直线为x,y,z轴建立空间直角坐标系,求出一些点的坐标,设EH=x,从而表示出HG=2-x,三棱锥B-GHE的高为AB=2,从而可表示出三棱锥B-GHE的体积V=$\frac{1}{3}[-(x-1)^{2}+1]$,从而看出x=1时V最大,这时G为AD中点.从而可求G点坐标,求出向量$\overrightarrow{BG}$坐标,可设平面BCD的法向量为$\overrightarrow{n}$={x,y,z},根据$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BC}=0}\\{\overrightarrow{n}•\overrightarrow{DC}=0}\end{array}\right.$即可求出$\overrightarrow{n}$,设直线BG与平面BCD所成角为θ,而根据sinθ=$|cos<\overrightarrow{n},\overrightarrow{BG}>|$求出sinθ.
解答 解:(Ⅰ)证明:∵AB∥CD,∠ABC=90°,CD=2AB=4;
又AE∥BC交CD于点E;
∴四边形ABCE是边长为2的正方形;
∴AC⊥BE,DE⊥AE;
又∵平面ADE⊥平面ABCE,平面ADE∩平面ABCE=AE;
∴DE⊥平面ABCE;
∵AC?平面ABCE,∴AC⊥DE;
又DE∩BE=E;
∴AC⊥平面DBE;
∵AC?平面DAC;
∴平面DAC⊥平面DEB;
(Ⅱ)由(Ⅰ)知DE⊥平面ABCE,AE⊥EC;
以E为原点,$\overrightarrow{EA}\;,\;\overrightarrow{EC}\;,\;\overrightarrow{ED}$的方向为x轴,y轴,z轴的正方向建立如图所示空间直角坐标系,则:
A(2,0,0),B(2,2,0),C(0,2,0),D(0,0,2);
设EH=x,则GH=DH=2-x(0<x<2);
∵AB∥CE,∴AB⊥面DAE;
∴${V_{B-GHE}}=\frac{1}{3}{S_{△GHE}}•AB=\frac{1}{3}[\frac{1}{2}x(2-x)]×2$=$\frac{1}{3}(-{x^2}+2x)=\frac{1}{3}[-{(x-1)^2}+1]$;
∵0<x<2,∴x=1时,三棱锥B-GHE体积最大,此时,H为ED中点;
∵GH∥AE,∴G也是AD的中点,∴G(1,0,1),$\overrightarrow{BG}=(-1\;,\;-2\;,\;1)$;
设$\overrightarrow n=(x\;,\;y\;,\;z)$是面BCD的法向量;
则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{BC}=(x\;,\;y\;,\;z)•(-2\;,\;0\;,\;0)=-2x=0\\ \overrightarrow n•\overrightarrow{DC}=(x\;,\;y\;,\;z)•(0\;,\;2\;,\;-2)=2y-2z=0\end{array}\right.$
令y=1,得$\overrightarrow n=(0\;,\;1\;,\;1)$;
设BG与面BCD所成角为θ;
则$sinθ=|cos<\overrightarrow{BG},\overrightarrow{n}>|=\frac{|\overrightarrow{BG}•\overrightarrow{n}|}{|\overrightarrow{BG}||\overrightarrow{n}|}=\frac{1}{\sqrt{6}•\sqrt{2}}$=$\frac{\sqrt{3}}{6}$;
∴BG与平面BCD所成角的正弦值为$\frac{{\sqrt{3}}}{6}$.
点评 考查对折叠前后图形的观察能力,面面垂直的性质定理,线面垂直的性质,线面垂直的判定定理,以及建立空间直角坐标系,利用空间向量解决线面角问题的方法,棱锥的体积公式,两非零向量垂直的充要条件,平面法向量的概念及求法,直线和平面所成角的概念,直线和平面所成角与直线和平面法向量夹角的关系,向量夹角余弦的坐标公式.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案| A. | $-\frac{29}{36}$ | B. | $\frac{29}{36}$ | C. | $\frac{11}{24}$ | D. | $-\frac{11}{24}$ |

| A. | 32 | B. | 48 | C. | 56 | D. | 96 |
| A. | (-1,-3) | B. | (1,-3) | C. | (1,3) | D. | (-1,3) |
上的动点,则点P到直线l1和到直线l2的距离之和的最小值是( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $2\sqrt{2}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |