题目内容
18．在△ABC中，a、b、c分别为角A、B、C所对应的三角形的边长，若4a$\overrightarrow{BC}$+2b$\overrightarrow{CA}$+3c$\overrightarrow{AB}$=$\overrightarrow{0}$，则cosB=（ ）| A． | $-\frac{29}{36}$ | B． | $\frac{29}{36}$ | C． | $\frac{11}{24}$ | D． | $-\frac{11}{24}$ |
分析 由已知及向量减法的平行四边形法则可得4a$\overrightarrow{BC}$+2b$\overrightarrow{CA}$+3c$\overrightarrow{AB}$=$\overrightarrow{0}$，即（4a-3c）$\overrightarrow{BC}$+（2b-3c）$\overrightarrow{CA}$=$\overrightarrow{0}$，根据向量的基本定理可得a，b，c之间的关系，然后利用余弦定理即可求cosB．
解答 解：∵4a$\overrightarrow{BC}$+2b$\overrightarrow{CA}$+3c$\overrightarrow{AB}$=$\overrightarrow{0}$，
∴（4a-3c）$\overrightarrow{BC}$+（2b-3c）$\overrightarrow{CA}$=$\overrightarrow{0}$，
∵$\overrightarrow{BC}$，$\overrightarrow{CA}$不共线
∴$\left\{\begin{array}{l}{4a-3c=0}\\{2b-3c=0}\end{array}\right.$即a=$\frac{3c}{4}$，b=$\frac{3c}{2}$，
则cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{\frac{9{c}^{2}}{16}+{c}^{2}-\frac{9{c}^{2}}{4}}{2×\frac{3c}{4}×c}$=-$\frac{11}{24}$；
故选D．
点评 本题主要考查了向量减法的四边形法则，平面向量的基本定理及余弦定理的综合应用，解题的关键是把已知变形为（4a-3c）$\overrightarrow{BC}$+（2b-3c）$\overrightarrow{CA}$=$\overrightarrow{0}$．
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
| A． | A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ | B． | C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | ||
| C． | C${\;}_{7}^{3}$--C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | D． | A${\;}_{7}^{3}$--A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ |
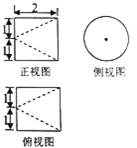
| A． | $\frac{π}{3}$cm3 | B． | $\frac{2π}{3}$cm3 | C． | πcm3 | D． | $\frac{4π}{3}$cm3 |
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象与y轴的交点为（0，1），它在y轴右侧的第一个最高点和第一个最低点的坐标分别为（x0，2）和（x0+2π，-2）则f（x）=2sin（$\frac{1}{2}$x+$\frac{π}{6}$）．