题目内容
16．已知圆的方程为x2+y2-2x-6y+1=0，那么圆心坐标为（ ）| A． | （-1，-3） | B． | （1，-3） | C． | （1，3） | D． | （-1，3） |
分析 将已知圆化成标准方程并对照圆标准方程的基本概念，即可得到所求圆心坐标．
解答 解：将圆x2+y2-2x-6y+1=0化成标准方程，得（x-1）2+（y-3）2=9，
∴圆表示以C（1，3）为圆心，半径r=3的圆．
故选：C．
点评 本题给出圆的一般方程，求圆心的坐标．着重考查了圆的标准方程与一般方程的知识，属于基础题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
6．有4名男医生、3名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有（ ）
| A． | A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ | B． | C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | ||
| C． | C${\;}_{7}^{3}$--C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | D． | A${\;}_{7}^{3}$--A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ |
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象与y轴的交点为（0，1），它在y轴右侧的第一个最高点和第一个最低点的坐标分别为（x0，2）和（x0+2π，-2）则f（x）=2sin（$\frac{1}{2}$x+$\frac{π}{6}$）．
11．
甲、乙两名同学8次数学测验成绩如茎叶图所示，$\overline{x}$1，$\overline{x}$2分别表示甲、乙两名同学8次数学测验成绩的平均数，s1，s2分别表示甲、乙两名同学8次数学测验成绩的标准差，则有（ ）
甲、乙两名同学8次数学测验成绩如茎叶图所示，$\overline{x}$1，$\overline{x}$2分别表示甲、乙两名同学8次数学测验成绩的平均数，s1，s2分别表示甲、乙两名同学8次数学测验成绩的标准差，则有（ ）| A． | $\overline{x}$1＞$\overline{x}$2，s1＜s2 | B． | $\overline{x}$1=$\overline{x}$2，s1＜s2 | C． | $\overline{x}$1=$\overline{x}$2，s1=s2 | D． | $\overline{x}$1＜$\overline{x}$2，s1＞s2 |
5．已知执行如图所示的程序框图，输出的S=485，则判断框内的条件可以是（ ）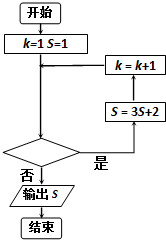
| A． | k＜5？ | B． | k＞7？ | C． | k≤5？ | D． | k≤6？ |