题目内容
20．已知以点P为圆心的圆经过点A（-1，1）和B（2，0），线段AB的垂直平分线交该圆于C、D两点，且|CD|=10（Ⅰ）求直线CD的方程；
（Ⅱ）求圆P的方程．
分析 （1）直接用点斜式求出直线CD的方程；
（2）根据条件得知|PA|为圆的半径，点P在直线CD上，列方程求得圆心P坐标，从而求出圆P的方程
解答 解：（1）直线AB的斜率k=-$\frac{1}{3}$，AB中点坐标为（$\frac{1}{2}$，$\frac{1}{2}$），…（3分）
∴直线CD的斜率为3，
方程为y-$\frac{1}{2}$=3（x-$\frac{1}{2}$）即3x-y-1=0；
（2）设圆心P（a，b），则由点P在直线CD上得：
3 a-b-1=0 ①…（8分）
又直径|CD|=10，
∴|PA|=5
∴（a+1）2+b2=25 ②…（10分）
由①②解得$\left\{\begin{array}{l}{a=2}\\{b=5}\end{array}\right.$或$\left\{\begin{array}{l}{a=-1}\\{b=-4}\end{array}\right.$
∴圆心P（2，5）或P（-1，-4）…（12分）
∴圆P的方程为（x-2）2+（y-5）2=25 或（x+1）2+（y+4）2=25…（14分
点评 此题考查直线方程的点斜式、圆的标准方程的求法．
练习册系列答案
相关题目
11．
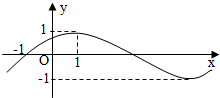已知函数f（x）=Asin（ωx+ϕ），x∈R（其中A＞0，ω＞0，-$\frac{π}{2}$＜ϕ＜$\frac{π}{2}$），其部分图象如下图所示，将f（x）的图象纵坐标不变，横坐标变成原来的$\frac{1}{2}$倍，再向右平移1个单位得到g（x）的图象，则函数g（x）的解析式为（ ）
已知函数f（x）=Asin（ωx+ϕ），x∈R（其中A＞0，ω＞0，-$\frac{π}{2}$＜ϕ＜$\frac{π}{2}$），其部分图象如下图所示，将f（x）的图象纵坐标不变，横坐标变成原来的$\frac{1}{2}$倍，再向右平移1个单位得到g（x）的图象，则函数g（x）的解析式为（ ）| A． | g（x）=sin$\frac{π}{8}$（x+1） | B． | g（x）=sin（$\frac{π}{2}$x-$\frac{π}{4}$） | C． | g（x）=sin（$\frac{π}{8}$x+1） | D． | g（x）=sin（$\frac{π}{2}$x+$\frac{π}{4}$） |
15．某学校有学生2500人，教师350人，后勤职工150人，为了调查对食堂服务的满意度，用分层抽样从中抽取300人，则学生甲被抽到的概率为（ ）
| A． | $\frac{1}{10}$ | B． | $\frac{1}{300}$ | C． | $\frac{1}{2500}$ | D． | $\frac{1}{3000}$ |
5．正方体ABCD-A1B1C1D1的棱长为1，M是棱AB的中点，点P是平面ABCD上的动点，且动点P到直线A1D1的距离与动点P到点M的距离的平方差为1，则动点P的轨迹是（ ）
| A． | 圆 | B． | 抛物线 | C． | 椭圆 | D． | 双曲线 |
12．已知△ABC，角A，B，C所对的边分别为a，b，c，则以下为钝角三角形的是（ ）
| A． | a=3，b=3，c=4 | B． | a=4，b=5，c=6 | C． | a=4，b=6，c=7 | D． | a=3，b=3，c=5 |
10．已知向量$\overrightarrow{a}$=（1，k），$\overrightarrow{b}$=（9，k-6），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则实数k的值为（ ）
| A． | -$\frac{3}{4}$ | B． | $\frac{3}{5}$ | C． | 3 | D． | 3+3$\sqrt{2}$ |