题目内容

5．正方体ABCD-A1B1C1D1的棱长为1，M是棱AB的中点，点P是平面ABCD上的动点，且动点P到直线A1D1的距离与动点P到点M的距离的平方差为1，则动点P的轨迹是（　　）
A．圆B．抛物线C．椭圆D．双曲线

分析 作PQ⊥AD，作QR⊥D1A1，PR即为点P到直线A1D1的距离，由勾股定理得PR2-PQ2=RQ2=1，又已知PR2-PM2=1，PM=PQ，即P到点M的距离等于P到AD的距离．

解答 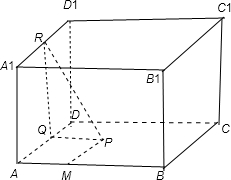解：如图所示：正方体ABCD-A1B1C1D1中，作PQ⊥AD，Q为垂足，
则PQ⊥面ADD1A1，过点Q作QR⊥D1A1，
则D1A1⊥面PQR，PR即为点P到直线A1D1的距离，由题意可得PR2-PQ2=RQ2=1．
又已知PR2-PM2=1，
∴PM=PQ，即P到点M的距离等于P到AD的距离，根据抛物线的定义可得，点P的轨迹是抛物线，
故选 B．

点评 本题考查抛物线的定义，求点的轨迹方程的方法，体现了数形结合的数学思想，得到PM=PQ是解题的关键．

练习册系列答案
相关题目
15．已知向量$\overrightarrow{i}$，$\overrightarrow{j}$，$\overrightarrow{k}$是空间直角坐标系Oxyz中，x轴，y轴，z轴正方向上的单位向量且$\overrightarrow{AB}$=-$\overrightarrow{i}$+$\overrightarrow{j}$-$\overrightarrow{k}$，则B的坐标是（-1，1，-1）．
16．已知函数f（x）=sinx+$\sqrt{3}$cosx，则下列命题正确的是①③④．（填上你认为正确的所有命题的序号）
①函数f（x）（x∈[0，$\frac{π}{2}$]）的单调递增区间是[0，$\frac{π}{6}$]；
②函数f（x）的图象关于点（-$\frac{π}{6}$，0）对称；
③函数f（x）的图象向左平移m（m＞0）个单位长度后，所得的图象关于y轴对称，则m的最小值是$\frac{π}{6}$；
④若实数m使得方程f（x）=m在[0，2π]上恰好有三个实数解x1，x2，x3，则x1+x2+x3=$\frac{7π}{3}$．
13．sin45°cos15°-cos135°sin165°=（　　）
A．-$\frac{1}{2}$B．-$\frac{\sqrt{3}}{2}$C．$\frac{1}{2}$D．$\frac{\sqrt{3}}{2}$
20．已知以点P为圆心的圆经过点A（-1，1）和B（2，0），线段AB的垂直平分线交该圆于C、D两点，且|CD|=10
（Ⅰ）求直线CD的方程；
（Ⅱ）求圆P的方程．
10．在△ABC中，角A，B，C所对的边分别为a，b，c，A=60°，b=2，△ABC的面积为4$\sqrt{3}$，则边c的值为（　　）
A．16B．16$\sqrt{3}$C．8D．8$\sqrt{3}$
17．已知数列{an}的前n项和为Sn=n（2n+1），则a10=39．
14．函数f（x）=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}（2x-3）}}$的定义域为（　　）
A．（$\frac{3}{2}$，+∞）B．（2，+∞）C．（0，$\frac{3}{2}$）D．（$\frac{3}{2}$，2）
15．连掷两次骰子分别得到点数m，n，向量$\overrightarrow{a}$=（m，n），$\overrightarrow{b}$=（-1，1），若△ABC中$\overrightarrow{AB}$与$\overrightarrow{a}$同向，$\overrightarrow{CB}$与$\overrightarrow{b}$反向，则∠ABC是钝角的概率是$\frac{5}{12}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网