题目内容

20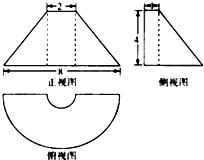．如图是某几何体的三视图，正视图是等腰梯形，俯视图中的曲线是两个同心的半圆组成的半圆环，侧视图是直角梯形，则该几何体的体积等于（　　）
A．12πB．16πC．20πD．24π

分析 由已知中的三视图，可知该几何体是一个半圆台挖去一个半圆柱的组合体，分别求出半圆台和半圆柱的体积，相减可得答案．

解答 解：根据几何体的三视图，得该几何体是一个半圆台挖去一个半圆柱的组合体，
半圆台的下底面为半径等于4，上底面为半径等于1，高为4，
半圆柱的底面为半径等于1，高为4，
∴该几何体的体积为V几何体=$\frac{1}{2}$×$\frac{1}{3}$×π（12+1×4+42）×4-$\frac{1}{2}$×π×12×4=12π．
故选：A．

点评 本题考查的知识点是简单空间图象的三视图，其中根据已知中的视图分析出几何体的形状及棱长是解答的关键．

练习册系列答案
相关题目
10．数列{an}满足an+1=$\left\{\begin{array}{l}{2{a}_{n}，（0≤an＜\frac{1}{2}）}\\{2{a}_{n}-1，（\frac{1}{2}≤{a}_{n}＜1）}\end{array}\right.$，若a1=$\frac{6}{7}$，则a2010=$\frac{3}{7}$．
11．点P为双曲线$\frac{x^2}{a^2}-\frac{y^2}{9}$=1的右支上任意一点，由P向两条渐近线作平行线交渐近线于M、N两点，若平行四边形OMPN面积为3，则双曲线的离心率为$\frac{\sqrt{13}}{2}$．
8．若函数f（x）与g（x）的图象关于直线y=x对称，已知函数f（x）=${（{\frac{1}{2}}）^{-x}}$，则f（2）+g（2）的值为（　　）
A．2B．3C．4D．5
15．在直角坐标系xOy 中，曲线C1的参数方程为$\left\{\begin{array}{l}x=1+cos2α\\ y=\frac{1}{2}cosα\end{array}$（α为参数），在极坐标系中，曲线C2的极坐标方程为ρsin（θ-$\frac{π}{4}$）=$\sqrt{2}$
（1）求曲线C2的普通方程
（2）设c1与c2相交于A，B两点，求|AB|的长．
5．已知平面α⊥β，α∩β=m，n?β，则“n⊥m”是“n⊥α”成立的（　　）
A．充要条件B．充分不必要条件
C．必要不充分条件D．既不充分也不必要条件
12．设i是虚数单位，a为实数，复数z=$\frac{1+ai}{i}$为纯虚数，则z的共轭复数为（　　）
A．-iB．iC．2iD．-2i
9．{an}是各项均为正数的等比数列，已a1=2，a3=8．
（Ⅰ）求数{an}的通项公式；          
（Ⅱ）求数{log2an}的前n项和Tn．
10．长方体的一个顶点上三条棱长分别为2，4，5，则它的表面积为（　　）
A．22B．40C．45D．76

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网