题目内容
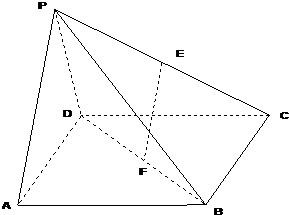
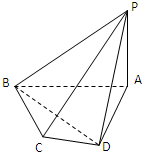
如图所示,四棱锥P-ABCD中,ABCD是矩形,三角形PAD为等腰直角三角形,∠APD=90°,面APD⊥面ABCD,AB=1,AD=2,E,F分别为PC和BD的中点.
(1)求证:EF∥平面PAD;
(2)证明:平面PAD⊥平面PDC;
(3)求四棱锥P-ABCD的体积.
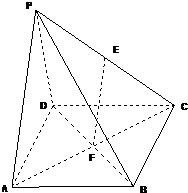
(1)求证:EF∥平面PAD;
(2)证明:平面PAD⊥平面PDC;
(3)求四棱锥P-ABCD的体积.

证明:(1)连AC,由题可知F在AC上,∵E,F分别是AC,PC的中点
∴EF∥PA
∵EF?平面PAD,PA?平面PAD
∴EF∥平面PAD(4分)
证明:(2)平面PAD⊥平面ABCD于AD,CD⊥AD,
∴CD⊥平面PAD,又CD?平面PDC,∴平面PAD⊥平面PDC(8分)
(3)过P作PO⊥AD于O∴PO⊥平面ABCD,
∵△PAD是等腰直角且AD=2,∴PO=1
∴VP-ABCD=
Sh=
(12分)
∴EF∥PA
∵EF?平面PAD,PA?平面PAD
∴EF∥平面PAD(4分)
证明:(2)平面PAD⊥平面ABCD于AD,CD⊥AD,
∴CD⊥平面PAD,又CD?平面PDC,∴平面PAD⊥平面PDC(8分)
(3)过P作PO⊥AD于O∴PO⊥平面ABCD,
∵△PAD是等腰直角且AD=2,∴PO=1
∴VP-ABCD=
| 1 |
| 3 |
| 2 |
| 3 |


练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目

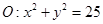 交于A、B两点,则
交于A、B两点,则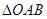 的最大面积为 .
的最大面积为 .