题目内容
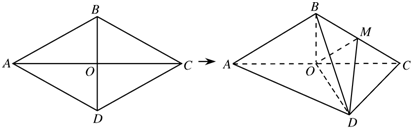
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2
.
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC;
(3)求三棱锥B-DOM的体积.
| 2 |
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC;
(3)求三棱锥B-DOM的体积.

(1)∵O为AC的中点,M为BC的中点,∴OM∥AB.
又∵OM?平面ABD,AB?平面ABD,
∴OM∥平面ABD.
(2)∵在菱形ABCD中,OD⊥AC,∴在三棱锥B-ACD中,OD⊥AC.
在菱形ABCD中,AB=AD=4,∠BAD=60°,可得BD=4.
∵O为BD的中点,∴DO=
BD=2.
∵O为AC的中点,M为BC的中点,∴OM=
AB=2.
因此,OD2+OM2=8=DM2,可得OD⊥OM.
∵AC、OM是平面ABC内的相交直线,
∴OD⊥平面ABC.
∵OD?平面DOM,
∴平面DOM⊥平面ABC.
(3)由(2)得,OD⊥平面BOM,所以OD是三棱锥D-BOM的高.
由OD=2,S△BOM=
×OB×BM×sin60°=
,
所以VB-DOM=VD-BOM=
S△BOM=×DO=
×
×2=
.

又∵OM?平面ABD,AB?平面ABD,
∴OM∥平面ABD.
(2)∵在菱形ABCD中,OD⊥AC,∴在三棱锥B-ACD中,OD⊥AC.
在菱形ABCD中,AB=AD=4,∠BAD=60°,可得BD=4.
∵O为BD的中点,∴DO=
| 1 |
| 2 |
∵O为AC的中点,M为BC的中点,∴OM=
| 1 |
| 2 |
因此,OD2+OM2=8=DM2,可得OD⊥OM.
∵AC、OM是平面ABC内的相交直线,
∴OD⊥平面ABC.
∵OD?平面DOM,
∴平面DOM⊥平面ABC.
(3)由(2)得,OD⊥平面BOM,所以OD是三棱锥D-BOM的高.
由OD=2,S△BOM=
| 1 |
| 2 |
| 3 |
所以VB-DOM=VD-BOM=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

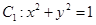 与圆
与圆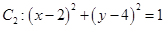 ,过动点
,过动点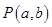 分别作圆
分别作圆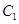 、圆
、圆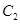 的切线
的切线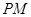 、
、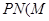 、
、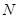 分别为切点),若
分别为切点),若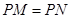 ,则
,则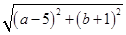 的最小值是 .
的最小值是 .