题目内容
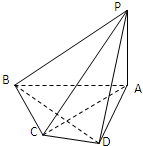
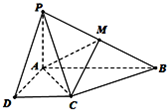
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
(Ⅰ)求证:平面PBD⊥平面PAC.
(Ⅱ)求四棱锥P-ABCD的体积V.
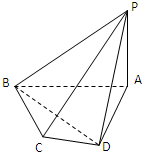
(Ⅰ)求证:平面PBD⊥平面PAC.
(Ⅱ)求四棱锥P-ABCD的体积V.

(Ⅰ)连接AC,∵BC=CD,AB=AD,
∴AC⊥BD,
又PA⊥平面ABCD,且BD?平面ABCD
∴PA⊥BD
又PA∩AC=A,
∴BD⊥平面PAC
又BD?平面BDP
∴平面PBD⊥平面PAC
(Ⅱ)依题意得∠CBD=∠CDB=30°,
又BC⊥AB,CD⊥AD,
所以∠DBA=∠BDA=60°
又BC=CD=a,
∴BD=
a
∴△ABD是边长为
a的正三角形
∴V=
(S△BCD+S△ABD)•PA=
(
•BC•CD•sin1200+
•AD•AB•sin600)•a
=
(
a2+
×3a2)•a=
a3
∴AC⊥BD,
又PA⊥平面ABCD,且BD?平面ABCD
∴PA⊥BD
又PA∩AC=A,
∴BD⊥平面PAC
又BD?平面BDP
∴平面PBD⊥平面PAC
(Ⅱ)依题意得∠CBD=∠CDB=30°,
又BC⊥AB,CD⊥AD,
所以∠DBA=∠BDA=60°
又BC=CD=a,
∴BD=
| 3 |
∴△ABD是边长为
| 3 |
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 6 |
| ||
| 2 |
| ||
| 2 |
| ||
| 3 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

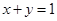 ,则
,则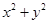 的最小值为 .
的最小值为 .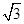 ,则k=( )
,则k=( )