Question

【题目】已知函数，曲线在点处切线与直线垂直.

（1）试比较与的大小，并说明理由；

（2）若函数有两个不同的零点，，证明：.

Answer 1

【答案】（1），理由见解析（2）详见解析

【解析】

（1）求出的导数，由两直线垂直的条件，即可得切线的斜率和切点坐标，进而可知的解析式和导数，求解单调区间，可得，即可得到与的大小；（2）运用分析法证明，不妨设，由根的定义化简可得，，要证：只需要证： ，求出，即证，令，即证，令，求出导数，判断单调性，即可得证.

（1）函数，，

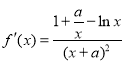所以，

又由切线与直线垂直，

可得，即，解得，

此时，

令，即，解得，

令，即，解得，

即有在上单调递增，在单调递减

所以

即

（2）不妨设，

由条件：

，

要证：只需要证：，

也即为，由

只需要证：，

设即证：，

设，则

在上是增函数，故，

即得证，所以.