题目内容
如图所示,正方体ABCDA1B1C1D1的棱长为6,则以正方体ABCDA1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为________.
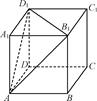

(18 +24)π
+24)π
 +24)π
+24)π设O为正方体外接球的球心,则O也是正方体的中心,O到平面AB1D1的距离是体对角线长的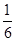 ,即为
,即为 .又球的半径是正方体对角线长的一半,即为3
.又球的半径是正方体对角线长的一半,即为3 ,由勾股定理可知,截面圆的半径为
,由勾股定理可知,截面圆的半径为 =2
=2 ,圆锥底面面积为S1=π·(2
,圆锥底面面积为S1=π·(2 )2=24π,圆锥的母线即为球的半径3
)2=24π,圆锥的母线即为球的半径3 ,圆锥的侧面积为S2=π×2
,圆锥的侧面积为S2=π×2 ×3
×3 =18
=18 π.因此圆锥的全面积为S=S2+S1=18
π.因此圆锥的全面积为S=S2+S1=18 π+24π=(18
π+24π=(18 +24)π.
+24)π.
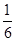 ,即为
,即为 .又球的半径是正方体对角线长的一半,即为3
.又球的半径是正方体对角线长的一半,即为3 ,由勾股定理可知,截面圆的半径为
,由勾股定理可知,截面圆的半径为 =2
=2 ,圆锥底面面积为S1=π·(2
,圆锥底面面积为S1=π·(2 )2=24π,圆锥的母线即为球的半径3
)2=24π,圆锥的母线即为球的半径3 ,圆锥的侧面积为S2=π×2
,圆锥的侧面积为S2=π×2 ×3
×3 =18
=18 π.因此圆锥的全面积为S=S2+S1=18
π.因此圆锥的全面积为S=S2+S1=18 π+24π=(18
π+24π=(18 +24)π.
+24)π.
练习册系列答案
相关题目
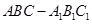 中,
中,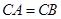 ,
,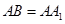 ,
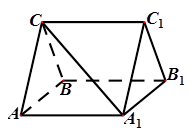
,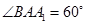 .
.
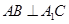 ;
; ,
,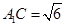 ,求三棱柱
,求三棱柱 ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
 的方向相同时,画出四棱锥P
的方向相同时,画出四棱锥P
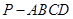 的五个顶点在同一球面上,若该正四棱锥的底面边长为2,侧棱长为
的五个顶点在同一球面上,若该正四棱锥的底面边长为2,侧棱长为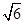 ,则这个球的表面积为_________.
,则这个球的表面积为_________.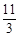 πa2
πa2 πa2
πa2
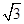 π
π ABC中,D,E,F分别是AB,AC,AA1的中点.设三棱锥F
ABC中,D,E,F分别是AB,AC,AA1的中点.设三棱锥F