题目内容
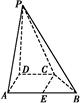
如图,在四棱锥P ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.

(1)当正视方向与向量 的方向相同时,画出四棱锥P
的方向相同时,画出四棱锥P ABCD的正视图(要求标出尺寸,并写出演算过程);
ABCD的正视图(要求标出尺寸,并写出演算过程);
(2)若M为PA的中点,求证:DM∥平面PBC;
(3)求三棱锥D PBC的体积.
PBC的体积.
 ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
(1)当正视方向与向量
 的方向相同时,画出四棱锥P
的方向相同时,画出四棱锥P ABCD的正视图(要求标出尺寸,并写出演算过程);
ABCD的正视图(要求标出尺寸,并写出演算过程);(2)若M为PA的中点,求证:DM∥平面PBC;
(3)求三棱锥D
 PBC的体积.
PBC的体积.(1)见解析 (2)见解析 (3)8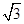
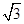
解:(1)在梯形ABCD中,过点C作CE⊥AB,垂足为E.
由已知得,四边形ADCE为矩形,
AE=CD=3,
在Rt△BEC中,
由BC=5,CE=4,
依勾股定理得
BE=3,
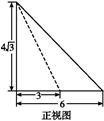
从而AB=6.
又由PD⊥平面ABCD,
得PD⊥AD,
从而在Rt△PDA中,
由AD=4,∠PAD=60°,
得PD=4
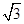 .
.正视图如图所示.
(2)取PB中点N,
连接MN,CN.
在△PAB中,
∵M是PA中点,
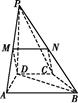
∴MN∥AB,MN=
 AB=3,
AB=3,又CD∥AB,CD=3,
∴MN∥CD,MN=CD,
∴四边形MNCD为平行四边形,
∴DM∥CN.
又DM
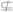 平面PBC,
平面PBC,CN?平面PBC,
∴DM∥平面PBC.
(3)
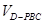 =
=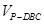 =
=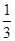 S△DBC·PD,
S△DBC·PD,又S△DBC=6,PD=4
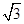 ,
,所以
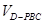 =8
=8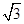 .
.
练习册系列答案
相关题目

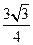
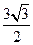
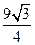
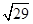 ,AC=BD=
,AC=BD=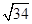 ,AD=BC=
,AD=BC=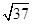 ,则四面体ABCD的外接球的表面积为( )
,则四面体ABCD的外接球的表面积为( )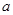 的三棱锥
的三棱锥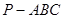 的侧面都是直角三角形,且四个顶点都在一个球面上,则球的表面积为( )
的侧面都是直角三角形,且四个顶点都在一个球面上,则球的表面积为( )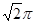

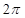
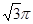
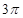
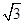 ,则正三棱锥SABC外接球的表面积是________.
,则正三棱锥SABC外接球的表面积是________.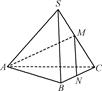
 ,则球的表面积为( )
,则球的表面积为( )




 ,该圆柱的表面积为________.
,该圆柱的表面积为________.