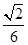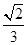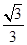题目内容
已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6,则该球的表面积为( )


| A.16π | B.24π | C.32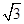 π π | D.48π |
D
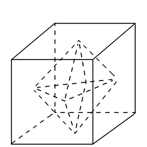
如图所示,

O为球心,O′为△ABC所在截面的圆心,E为AD中点.|OE|=|O′A|=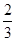 ×3×
×3×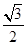 =
=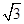 ,|AE|=3,所以球的半径|OA|=2
,|AE|=3,所以球的半径|OA|=2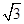 ,所以所求的球的表面积为4π(2
,所以所求的球的表面积为4π(2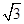 )2=48π.
)2=48π.

O为球心,O′为△ABC所在截面的圆心,E为AD中点.|OE|=|O′A|=
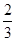 ×3×
×3×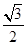 =
=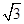 ,|AE|=3,所以球的半径|OA|=2
,|AE|=3,所以球的半径|OA|=2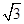 ,所以所求的球的表面积为4π(2
,所以所求的球的表面积为4π(2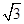 )2=48π.
)2=48π.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
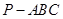 中,
中,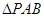 和
和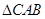 都是以
都是以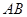 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,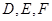 分别是
分别是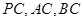 的中点.
的中点.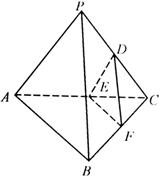
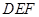 //平面
//平面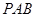 ;
;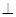
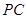 ;
;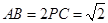 ,求三棱锥
,求三棱锥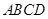 的边长为2,
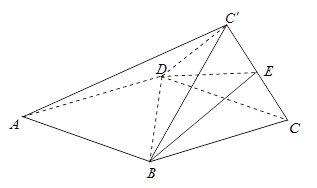
的边长为2, 为正三角形,现将
为正三角形,现将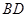 向上折起,折起后的点
向上折起,折起后的点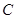 记为
记为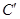 ,且
,且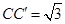 ,连接
,连接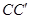 .
.
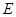 为
为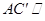 平面
平面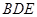 ;
;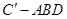 的体积.
的体积.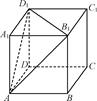
 ,则球的体积为 .
,则球的体积为 .  ,则球的表面积为( )
,则球的表面积为( )




 的正方形,则以该空间几何体各个面的中心为顶点的多面体的体积为( ).
的正方形,则以该空间几何体各个面的中心为顶点的多面体的体积为( ).