题目内容
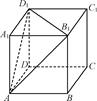
在如图所示的多面体中,已知正三棱柱ABCA1B1C1的所有棱长均为2,四边形ABDC是菱形.

(1)求证:平面ADC1⊥平面BCC1B1;
(2)求该多面体的体积.

(1)求证:平面ADC1⊥平面BCC1B1;
(2)求该多面体的体积.
(1)见解析(2)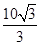
(1)证明:由正三棱柱ABCA1B1C1,得BB1⊥AD.
而四边形ABDC是菱形,所以AD⊥BC.
又BB1 平面BB1C1C,BC
平面BB1C1C,BC 平面BB1C1C,且BC∩BB1=B,所以AD⊥平面BCC1B1.
平面BB1C1C,且BC∩BB1=B,所以AD⊥平面BCC1B1.
又由AD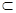 平面ADC1,得平面ADC1⊥平面BCC1B1.
平面ADC1,得平面ADC1⊥平面BCC1B1.
(2)解:因为正三棱柱ABCA1B1C1的体积为V1=S△ABC×AA1=2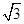 ,
,
四棱锥DB1C1CB的体积为V2=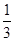 S平面BCC1B1×
S平面BCC1B1×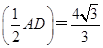 ,
,
所以该多面体的体积为V=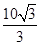 .
.
而四边形ABDC是菱形,所以AD⊥BC.
又BB1
 平面BB1C1C,BC
平面BB1C1C,BC 平面BB1C1C,且BC∩BB1=B,所以AD⊥平面BCC1B1.
平面BB1C1C,且BC∩BB1=B,所以AD⊥平面BCC1B1.又由AD
 平面ADC1,得平面ADC1⊥平面BCC1B1.
平面ADC1,得平面ADC1⊥平面BCC1B1.(2)解:因为正三棱柱ABCA1B1C1的体积为V1=S△ABC×AA1=2
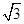 ,
,四棱锥DB1C1CB的体积为V2=
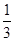 S平面BCC1B1×
S平面BCC1B1×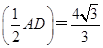 ,
,所以该多面体的体积为V=
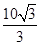 .
.
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
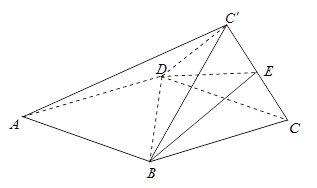
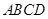 的边长为2,
的边长为2, 为正三角形,现将
为正三角形,现将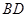 向上折起,折起后的点
向上折起,折起后的点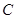 记为
记为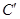 ,且
,且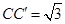 ,连接
,连接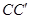 .
.
 为
为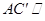 平面
平面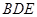 ;
;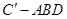 的体积.
的体积.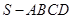 中,底面
中,底面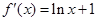 是直角梯形,
是直角梯形,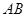
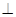
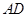 ,
, 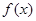 ,侧棱
,侧棱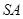
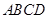 ,且
,且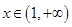 ,则点
,则点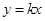 到平面
到平面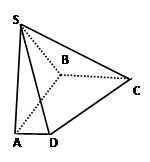
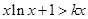
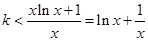
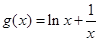
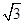 ,则正三棱锥SABC外接球的表面积是________.
,则正三棱锥SABC外接球的表面积是________.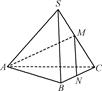
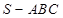 中,
中,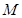 、
、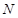 分别是棱
分别是棱 、
、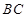 的中点,且
的中点,且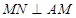 ,若侧棱
,若侧棱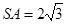 ,则正三棱锥
,则正三棱锥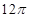
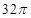
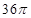
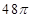
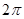 ,该圆柱的表面积为________.
,该圆柱的表面积为________.