题目内容
3．设每门高射炮命中飞机的概率为0.6，两门高射炮同时射击一发炮弹，则飞机被命中的概率为0.84．分析 先求出目标没有被击中的概率，即两门高射炮都没有击中目标的概率，再用1减去此概率，即得所求．
解答 解：∵每门高射炮命中飞机的概率为0.6，
∴两门高射炮同时射击一发炮弹，飞机标没有被击中的概率为 （1-0.6）（1-0.6）=0.16，
故飞机被击中的概率为1-0.16=0.84．
故答案为：0.84
点评 本题主要考查相互独立事件的概率乘法公式，所求的事件的概率与它的对立事件的概率之间的关系，属于基础题．
练习册系列答案
相关题目
14．下图几何体是由选项中的哪个平面图旋转而得到的（ ）
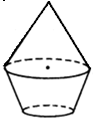
| A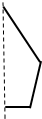． |  | B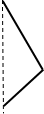． |  | C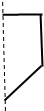． |  | D． |  |
15．小明家1～4月份用电量的一组数据如下：
由散点图可知，用电量y与月份x之间有较好的线性相关关系，其线性回归直线方程是$\widehat{y}$═-7x+$\widehat{a}$，则$\widehat{a}$等于（ ）
| 月份x | 1 | 2 | 3 | 4 |
| 用电量y | 45 | 40 | 30 | 25 |
| A． | 105 | B． | 51.5 | C． | 52 | D． | 52.5 |
12．在△ABC中，若∠B=30°，AB=2$\sqrt{3}$，AC=2，则△ABC的面积为（ ）
| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$或$\sqrt{2}$ | C． | 2$\sqrt{3}$或$\sqrt{3}$ | D． | 2$\sqrt{3}$ |
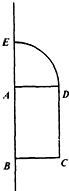如图所示，矩形ABCD和一个圆心角为90°的扇形拼在一起，其中AB=2，BC=AE=1，则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为（ ）