题目内容
13.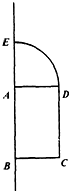 如图所示,矩形ABCD和一个圆心角为90°的扇形拼在一起,其中AB=2,BC=AE=1,则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为( )
如图所示,矩形ABCD和一个圆心角为90°的扇形拼在一起,其中AB=2,BC=AE=1,则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为( )| A. | 7π | B. | 5π | C. | 9π | D. | 8π |
分析 以AB所在直线为旋转轴将整个图形旋转一周所得几何体是一个半球与圆柱的组合体,计算各个面的面积相加可得答案.
解答 解:由已知可得:以AB所在直线为旋转轴将整个图形旋转一周所得几何体是一个半球与圆柱的组合体,
半球的半径和圆柱底面的半径为1,圆柱的高为2,
故半球面的面积为:2πr2=2π,
圆柱的底面面积为:πr2=π,
圆柱的侧面积为:2πrh=4π,
故组合体的表面积为:7π,
故选:A
点评 本题考查的知识点是旋转体,球和圆柱的表面积公式,难度不大,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
4.“孝敬父母.感恩社会”是中华民族的传统美德.从出生开始,父母就对们关心无微不至,其中对我们物质帮助是最重要的一个指标,下表是一个统计员在统计《父母为我花了多少》当中使用处理得到下列的数据:
参考数据公式:$\sum_{i=1}^6{x_i}{y_i}$=1024.6,$\sum_{i=1}^6{{x_i}^2}$=730,
线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,($\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{n=i}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$)
假设花费累积y与岁数x符合线性相关关系,求
(1)花费累积y与岁数x的线性回归直线方程(系数保留3位小数);
(2)24岁大学毕业之后,我们不再花父母的钱,假设你在30岁成家立业之后,在你50岁之前偿还父母为你的花费(不计利息).那么你每月要偿还父母约多少元钱?
参考数据公式:$\sum_{i=1}^6{x_i}{y_i}$=1024.6,$\sum_{i=1}^6{{x_i}^2}$=730,
线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,($\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{n=i}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$)
| 岁数x | 1 | 2 | 6 | 12 | 16 | 17 |
| 花费累积y(万元) | 1 | 2.8 | 9 | 17 | 22 | 24 |
(1)花费累积y与岁数x的线性回归直线方程(系数保留3位小数);
(2)24岁大学毕业之后,我们不再花父母的钱,假设你在30岁成家立业之后,在你50岁之前偿还父母为你的花费(不计利息).那么你每月要偿还父母约多少元钱?
8.a,b表示直线,α表示平面,则下列命题中正确的是( )
| A. | $\left.\begin{array}{l}{a∥b}\\{b⊥α}\end{array}\right\}$⇒a⊥α | B. | $\left.\begin{array}{l}{a∥b}\\{b?α}\end{array}\right\}$⇒a∥α | C. | $\left.\begin{array}{l}{a⊥b}\\{b∥α}\end{array}\right\}$⇒a⊥α | D. | $\left.\begin{array}{l}{a⊥α}\\{a⊥b}\end{array}\right\}$⇒b?α |
18.某高中的4名高三学生计划在高考结束后到西藏、新疆、香港等3个地区去旅游,要求每个地区都要有学生去,每个学生只去一个地区旅游,且学生甲不到香港,则不同的出行安排有( )
| A. | 36种 | B. | 28种 | C. | 24种 | D. | 22种 |
2.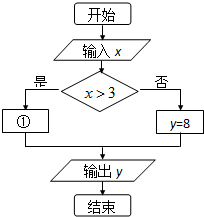 在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )
在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )
 在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )
在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )| A. | y=8+2.6x | B. | y=9+2.6x | C. | y=8+2.6(x-3) | D. | y=9+2.6(x-3) |
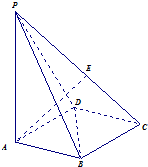 如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.
如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.