题目内容
双曲线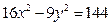 的左、右两个焦点分别为
的左、右两个焦点分别为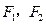 ,点
,点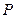 在双曲线上,且
在双曲线上,且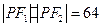 ,求
,求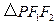 的面积.
的面积.
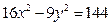 的左、右两个焦点分别为
的左、右两个焦点分别为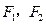 ,点
,点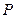 在双曲线上,且
在双曲线上,且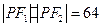 ,求
,求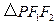 的面积.
的面积.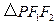 的面积
的面积
双曲线方程可化为 ,
, .
.
由双曲线定义知 .
.
又 ,
,
 在
在 中,由余弦定理得
中,由余弦定理得


 .
.

 .
.
 ,
, .
.由双曲线定义知
 .
.又
 ,
, 在
在 中,由余弦定理得
中,由余弦定理得

 .
.
 .
.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
题目内容
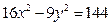 的左、右两个焦点分别为
的左、右两个焦点分别为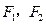 ,点
,点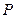 在双曲线上,且
在双曲线上,且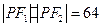 ,求
,求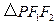 的面积.
的面积.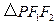 的面积
的面积
 ,
, .
. .
. ,
, 在
在 中,由余弦定理得
中,由余弦定理得

 .
.
 .
.
 备战中考寒假系列答案
备战中考寒假系列答案