题目内容
5. 如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,△BCF是正三角形,EF∥AB,EF=2,则该多面体的体积为( )
如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,△BCF是正三角形,EF∥AB,EF=2,则该多面体的体积为( )| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | 2 |
分析 该几何体是一个三棱柱截取两个四棱锥,体积相减即为该多面体的体积.
解答 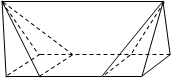 解:一个完整的三棱柱的图象为:棱柱的高为2;
解:一个完整的三棱柱的图象为:棱柱的高为2;
底面三角形的底为1,高为:$\frac{\sqrt{2}}{2}$,
其体积为:$\frac{1}{2}×1×\frac{\sqrt{2}}{2}×2$=$\frac{\sqrt{2}}{2}$;
割去的四棱锥体积为:$\frac{1}{3}×1×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{6}$,
所以,几何体的体积为:$\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{6}=\frac{\sqrt{2}}{3}$,
故选:B.
点评 本题考查学生的空间想象能力,几何体的添补,是基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
20.函数f(x)=$\left\{\begin{array}{l}{{a}^{x},(x>1)}\\{(4-\frac{a}{2})x+5,(x≤1)}\end{array}\right.$满足对任意x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0成立,则实数a的取值范围是( )
| A. | (4,+∞) | B. | [6,8) | C. | (6,8) | D. | (1,8) |
14.函数 y=cos2x+2cosx的值域是( )
| A. | [-1,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-\frac{3}{2},-1]$ | D. | $[\frac{3}{2},3]$ |
 如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.