题目内容
10. 如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD;
(3)求三棱锥B-ADF的体积.
分析 (1)连接AC交BD于点G,连接EG.通过中位线定理及线面平行的判定定理即得结论;
(2)证明DE⊥平面PBC,可得DE⊥PB,又EF⊥PB且DE∩EF=E,所以PB⊥平面EFD;
(3)利用等体积法,求三棱锥B-ADF的体积.
解答  证明:(1)连接AC交BD于点G,连接EG.(1分)
证明:(1)连接AC交BD于点G,连接EG.(1分)
因为四边形ABCD是正方形,所以点G是AC的中点,
又因为E为PC的中点,因此EG∥PA.(2分)
而EG?平面EDB,所以PA∥平面EDB.(3分)
(2)证明:∵PD⊥底面ABCD且DC?底面ABCD,∴PD⊥DC
∵PD=DC,可知△PDC是等腰直角三角形,而DE是斜边PC的中线,
∴DE⊥PC①
同样由PD⊥底面ABCD,得PD⊥BC
∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC
而DE?平面PDC,∴BC⊥DE②
由①和②推得DE⊥平面PBC
而PB?平面PBC,∴DE⊥PB
又EF⊥PB且DE∩EF=E,所以PB⊥平面EFD…(8分)
(3)解:过点F作FH∥PD,交BD于H.
因为PD⊥底面ABCD,FH∥PD,所以FH⊥底面ABCD.
由题意,可得$PB=\sqrt{3}$,$PC=\sqrt{2}$,$PE=\frac{{\sqrt{2}}}{2}$.
由Rt△PFE∽Rt△PCF,得$\frac{PF}{PE}=\frac{PC}{PB}$,$PF=\frac{PE•PC}{PB}=\frac{{\sqrt{3}}}{3}$.
由Rt△BFH∽Rt△BPD,得$\frac{BF}{BP}=\frac{FH}{PD}$,$FH=\frac{BF•PD}{BP}=\frac{2}{3}$.
所以${V_{F-ABD}}=\frac{1}{3}{S_{△ABD}}•FH=\frac{1}{3}×\frac{1}{2}×1×1×\frac{2}{3}=\frac{1}{9}$,(11分)
所以${V_{B-ADF}}={V_{F-ABD}}=\frac{1}{9}$,即三棱锥B-ADF的体积为$\frac{1}{9}$…(12分)
点评 本题考查间中线面垂直、线面平行的判定定理,三棱锥B-ADF的体积,考查学生分析解决问题的能力,属于中档题.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,△BCF是正三角形,EF∥AB,EF=2,则该多面体的体积为( )
如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,△BCF是正三角形,EF∥AB,EF=2,则该多面体的体积为( )| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | 2 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
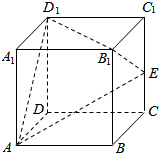 在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )
在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )| A. | $\frac{3}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{11}{12}$ | D. | $\frac{23}{24}$ |