题目内容
17．已知直线Ax+y+C=0，其中A，C，4成等比数列，且直线经过抛物线y2=8x的焦点，则A+C=（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 4 |
分析 根据A，C，4成等比数列，利用等比数列的性质列出关系式，找出已知抛物线的焦点坐标代入直线解析式得到关系式，联立求出A与C的值，即可确定出A+C的值．
解答 解：∵A，C，4成等比数列，
∴C2=4A①，
∵直线Ax+y+C=0经过抛物线y2=8x的焦点，焦点为（2，0），
∴2A+C=0②，
联立①②，解得：A=1，C=-2或A=C=0（舍去），
则A+C=1-2=-1，
故选：A．
点评 此题考查了抛物线的简单性质，熟练掌握抛物线的简单性质是解本题的关键．
练习册系列答案
相关题目
5．
如图，在多面体ABCDEF中，已知ABCD是边长为1的正方形，且△ADE，△BCF是正三角形，EF∥AB，EF=2，则该多面体的体积为（ ）
如图，在多面体ABCDEF中，已知ABCD是边长为1的正方形，且△ADE，△BCF是正三角形，EF∥AB，EF=2，则该多面体的体积为（ ）| A． | $\sqrt{2}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{{2\sqrt{2}}}{3}$ | D． | 2 |
2．
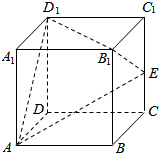在棱长为1的正方体ABCD-A1B1C1D1中，E是棱CC1的中点，F是侧面BCC1B1内（包括边）的动点，且A1F∥平面D1AE，沿A1F运动，将B1点所在的几何体削去，则剩余几何体的体积为（ ）
在棱长为1的正方体ABCD-A1B1C1D1中，E是棱CC1的中点，F是侧面BCC1B1内（包括边）的动点，且A1F∥平面D1AE，沿A1F运动，将B1点所在的几何体削去，则剩余几何体的体积为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{7}{8}$ | C． | $\frac{11}{12}$ | D． | $\frac{23}{24}$ |