题目内容
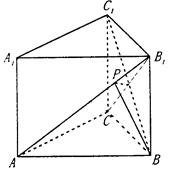
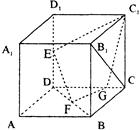
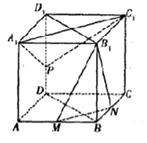
(本题满分12分)如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°.BC=CC1=a,AC=2a.
(I)求证:AB1⊥BC1;
(II)求二面角B—AB1—C的大小;
(III)求点A1到平面AB1C的距离.
(I)求证:AB1⊥BC1;
(II)求二面角B—AB1—C的大小;
(III)求点A1到平面AB1C的距离.
|
(1)略
(2)
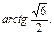
(3)

(1)证明:∵ABC—A1B1C1是直三棱柱,
∴CC1⊥平面ABC, ∴AC⊥CC1.
∵AC⊥BC, ∴AC⊥平面B1BCC1.
∴B1C是AB1在平面B1BCC1上的射影.
∵BC=CC1, ∴四边形B1BCC1是正方形,
∴BC1⊥B1C. 根据三垂线定理得,
AB1⊥BC1.………………5分
(2)解:设BC1∩B1C=O,作OP⊥AB1于点P,
连结BP.∵BO⊥AC,且BO⊥B1 C,
∴BO⊥平面AB1C.
∴OP是BP在平面AB1C上的射影.
根据三垂线定理得,AB1⊥BP.
∴∠OPB是二面角B—AB1—C的平面角.…………8分
∵△OPB1~△ACB1, ∴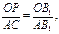 ∴
∴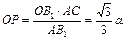
在Rt△POB中,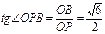 ,
,
∴二面角B—AB1—C的大小为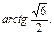 …………10分
…………10分
(3)解:[解法1] ∵A1C1//AC,A1C1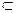 平面AB1C,
平面AB1C,
∴A1C1//平面AB1C.
∴点A1到平面AB1C的距离与点C1到平面AB1C.的距离相等.
∵BC1⊥平面AB1C,
∴线段C1O的长度为点A1到平面AB1C的距离.
∴点A1到平面AB1C的距离为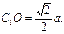 …………14分
…………14分
[解法2]连结A1C,有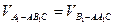 ,设点A1到平面AB1C的距离为h.
,设点A1到平面AB1C的距离为h.
∵B1C1⊥平面ACC1A1, ∴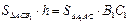 ,
,
又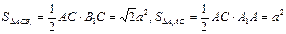 ,
,
∴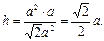 ∴点A1到平面AB1C的距离为
∴点A1到平面AB1C的距离为 …………14分
…………14分
∴CC1⊥平面ABC, ∴AC⊥CC1.
∵AC⊥BC, ∴AC⊥平面B1BCC1.
∴B1C是AB1在平面B1BCC1上的射影.
∵BC=CC1, ∴四边形B1BCC1是正方形,
∴BC1⊥B1C. 根据三垂线定理得,
AB1⊥BC1.………………5分
(2)解:设BC1∩B1C=O,作OP⊥AB1于点P,
连结BP.∵BO⊥AC,且BO⊥B1 C,
∴BO⊥平面AB1C.
∴OP是BP在平面AB1C上的射影.
根据三垂线定理得,AB1⊥BP.
∴∠OPB是二面角B—AB1—C的平面角.…………8分
∵△OPB1~△ACB1, ∴
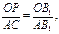 ∴
∴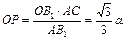
在Rt△POB中,
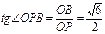 ,
,∴二面角B—AB1—C的大小为
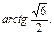 …………10分
…………10分(3)解:[解法1] ∵A1C1//AC,A1C1
 平面AB1C,
平面AB1C,∴A1C1//平面AB1C.
∴点A1到平面AB1C的距离与点C1到平面AB1C.的距离相等.
∵BC1⊥平面AB1C,
∴线段C1O的长度为点A1到平面AB1C的距离.
∴点A1到平面AB1C的距离为
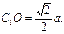 …………14分
…………14分[解法2]连结A1C,有
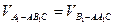 ,设点A1到平面AB1C的距离为h.
,设点A1到平面AB1C的距离为h.∵B1C1⊥平面ACC1A1, ∴
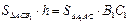 ,
,又
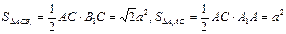 ,
,∴
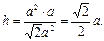 ∴点A1到平面AB1C的距离为
∴点A1到平面AB1C的距离为 …………14分
…………14分
练习册系列答案
相关题目
 CD垂直,已知BC=2AD=4,
CD垂直,已知BC=2AD=4, ,
,
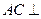 面ABF;
面ABF;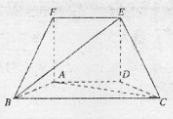
 .
. 
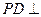 平面
平面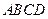 ,
,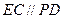 ,且
,且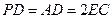 ="2" .
="2" .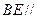 平面
平面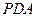 .
. 

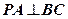 ;
;
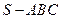 ,若空间一点
,若空间一点 满足
满足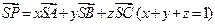 ,则
,则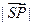 的最小值为
的最小值为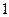

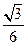
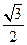
 是夹角为
是夹角为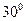 的异面直线,则满足条件“
的异面直线,则满足条件“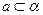 ,
,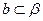 ,且
,且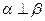 ”的平面
”的平面 ,
, ( )
( )