题目内容
(本小题满分14分)
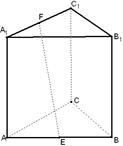
如图,在直四棱柱ABCD-A B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, "
中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, "
AA ="2, " E、E
="2, " E、E 分别是棱AD、AA
分别是棱AD、AA 的中点.
的中点. 

(1)设F是棱AB的中点,证明:直线EE //平面FCC
//平面FCC ;
;
(2)证明:平面D1AC⊥平面BB1C1C.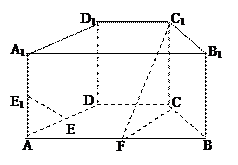
如图,在直四棱柱ABCD-A
 B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, "
中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, " AA
 ="2, " E、E
="2, " E、E 分别是棱AD、AA
分别是棱AD、AA 的中点.
的中点. 

(1)设F是棱AB的中点,证明:直线EE
 //平面FCC
//平面FCC ;
;(2)证明:平面D1AC⊥平面BB1C1C.

略
证明:(1)在直四棱柱ABCD-A B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,
连接A1D,C1F1,CF1,因为AB="4," CD=2,且AB//CD,
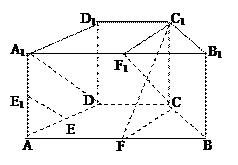
所以CDA1F1,A1F1CD为平行四边形, ………2分
所以CF1//A1D,
又因为E、E 分别是棱AD、AA
分别是棱AD、AA 的中点,
的中点,
所以EE1//A1D, ………3分
所以CF1//EE1, ………4分
又因为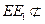 平面FCC
平面FCC , ………5分
, ………5分
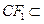 平面FCC
平面FCC , ………6分
, ………6分
所以直线EE //平面FCC
//平面FCC . ………7分
. ………7分
(2)连接AC,在直棱柱中,CC1⊥平面ABCD,AC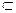 平面ABCD,
平面ABCD,
所以CC1⊥AC, ………8分
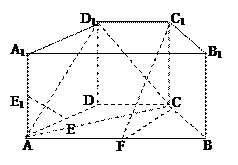
因为底面ABCD为等腰梯形,AB="4," BC=2,
F是棱AB的中点,所以CF=CB=BF,
△BCF为正三角形,………10分
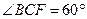 ,△ACF为等腰三角形,且
,△ACF为等腰三角形,且
所以AC⊥BC,
又因为BC与CC1都在平面BB1C1C内且交于点C,
所以AC⊥平面BB1C1C, ………12分
而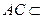 平面D1AC, ………13分
平面D1AC, ………13分
所以平面D1AC⊥平面BB1C1C. ………………………14分
 B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,连接A1D,C1F1,CF1,因为AB="4," CD=2,且AB//CD,

所以CDA1F1,A1F1CD为平行四边形, ………2分
所以CF1//A1D,
又因为E、E
 分别是棱AD、AA
分别是棱AD、AA 的中点,
的中点,所以EE1//A1D, ………3分
所以CF1//EE1, ………4分
又因为
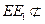 平面FCC
平面FCC , ………5分
, ………5分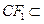 平面FCC
平面FCC , ………6分
, ………6分所以直线EE
 //平面FCC
//平面FCC . ………7分
. ………7分(2)连接AC,在直棱柱中,CC1⊥平面ABCD,AC
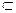 平面ABCD,
平面ABCD,
所以CC1⊥AC, ………8分
因为底面ABCD为等腰梯形,AB="4," BC=2,
F是棱AB的中点,所以CF=CB=BF,
△BCF为正三角形,………10分
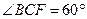 ,△ACF为等腰三角形,且
,△ACF为等腰三角形,且
所以AC⊥BC,
又因为BC与CC1都在平面BB1C1C内且交于点C,
所以AC⊥平面BB1C1C, ………12分
而
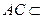 平面D1AC, ………13分
平面D1AC, ………13分所以平面D1AC⊥平面BB1C1C. ………………………14分

练习册系列答案
相关题目
 平面
平面 ,
, ,且
,且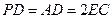 ="2" .
="2" .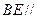 平面
平面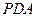 .
. 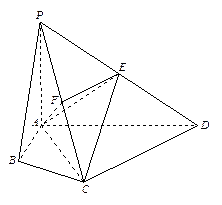
 中,
中,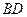 为AC边上的高,
为AC边上的高,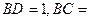
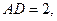 沿BD将
沿BD将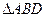 翻折,使得
翻折,使得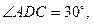 得到几何体
得到几何体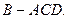
 ABC=90°,BC=2,AB=4,CC1=4,E在BB1上,且EB1=1,D、F分别为CC1、A1C1的中点。
ABC=90°,BC=2,AB=4,CC1=4,E在BB1上,且EB1=1,D、F分别为CC1、A1C1的中点。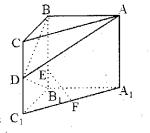
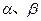 是两个不重合的平面,
是两个不重合的平面,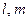 为不重合的直线,则下列命题正确的( )
为不重合的直线,则下列命题正确的( ) 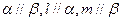 ,则
,则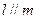
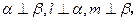 ,则
,则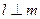
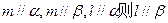
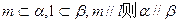
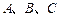 在球心为
在球心为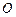 的球面上,
的球面上,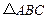 的内角
的内角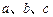 ,且
,且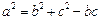 ,
,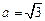 ,球心
,球心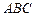 的距离为
的距离为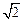 ,则该球的表面积为 .
,则该球的表面积为 .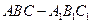 的各棱长都为2,E,F分别是
的各棱长都为2,E,F分别是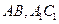 的中点,则EF的长是 ( )
的中点,则EF的长是 ( )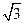
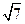
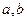 是夹角为
是夹角为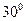 的异面直线,则满足条件“
的异面直线,则满足条件“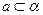 ,
,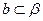 ,且
,且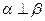 ”的平面
”的平面 ,
,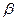 ( )
( )