题目内容
已知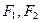 为椭圆的左右焦点,抛物线以
为椭圆的左右焦点,抛物线以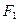 为顶点,
为顶点,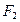 为焦点,设
为焦点,设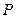 为椭圆与抛物线的一个交点,椭圆离心率为
为椭圆与抛物线的一个交点,椭圆离心率为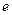 ,且
,且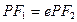 ,求
,求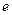 的值
的值
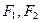 为椭圆的左右焦点,抛物线以
为椭圆的左右焦点,抛物线以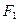 为顶点,
为顶点,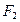 为焦点,设
为焦点,设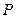 为椭圆与抛物线的一个交点,椭圆离心率为
为椭圆与抛物线的一个交点,椭圆离心率为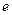 ,且
,且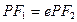 ,求
,求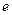 的值
的值
如图:
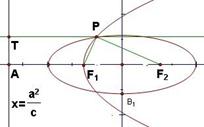
过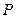 作椭圆的左准线的垂线,垂足为
作椭圆的左准线的垂线,垂足为
则 ,所以
,所以
所以椭圆的左准线即为抛物线的准线
所以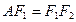 ,即
,即 ,所以
,所以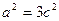 ,
,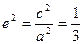 ,
,

过
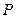 作椭圆的左准线的垂线,垂足为
作椭圆的左准线的垂线,垂足为
则
 ,所以
,所以
所以椭圆的左准线即为抛物线的准线
所以
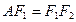 ,即
,即 ,所以
,所以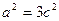 ,
,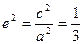 ,
,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
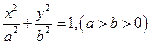 的左右焦点分别为
的左右焦点分别为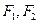 ,离心率
,离心率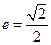 ,右准线为
,右准线为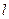 ,
,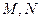 是
是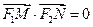 。
。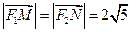 ,求
,求 的值;
的值;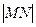 取最小值时,
取最小值时,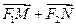 与
与 共线。
共线。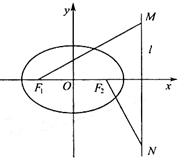
 分别是椭圆
分别是椭圆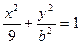
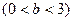 的左右焦点,若在其右准线上存在点
的左右焦点,若在其右准线上存在点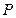
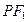 的垂直平分线恰好经过
的垂直平分线恰好经过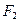 ,求
,求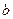 的取值范围
的取值范围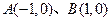 ,直线
,直线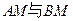 相交于点
相交于点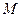 ,且它们的斜率之积为
,且它们的斜率之积为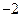 ,
,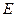 的方程;
的方程;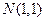 的直线
的直线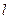 与曲线
与曲线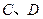 两点,且
两点,且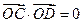 ,求直线
,求直线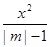 +
+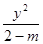 =1表示焦点在y轴上的椭圆,则m的取值范围是 ( )
=1表示焦点在y轴上的椭圆,则m的取值范围是 ( )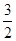
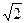 , BC="1." 以AB的中点
, BC="1." 以AB的中点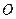 为原点建立如图8所示的平面直角坐标系
为原点建立如图8所示的平面直角坐标系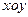 .
. 交(Ⅰ)中椭圆于M,N两点,是否存在直线
交(Ⅰ)中椭圆于M,N两点,是否存在直线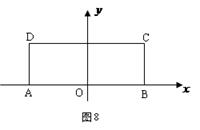
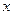 轴上的椭圆与
轴上的椭圆与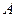 ,与
,与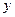 轴的正半轴交于点
轴的正半轴交于点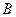 ,
,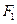 是左焦点且
是左焦点且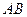 的距离
的距离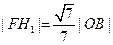 ,求椭圆的离心率.
,求椭圆的离心率.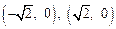 ,则PC·PD的最大值为 ( )
,则PC·PD的最大值为 ( )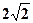 C 3 D
C 3 D 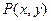 是椭圆
是椭圆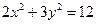 上的一个动点,则
上的一个动点,则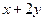 的最大值为( )
的最大值为( )