题目内容
已知中心在原点,焦点在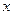 轴上的椭圆与
轴上的椭圆与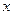 轴的负半轴交于点
轴的负半轴交于点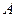 ,与
,与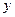 轴的正半轴交于点
轴的正半轴交于点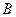 ,
,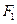 是左焦点且
是左焦点且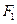 到直线
到直线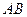 的距离
的距离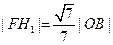 ,求椭圆的离心率.
,求椭圆的离心率.
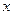 轴上的椭圆与
轴上的椭圆与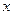 轴的负半轴交于点
轴的负半轴交于点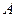 ,与
,与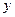 轴的正半轴交于点
轴的正半轴交于点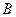 ,
,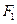 是左焦点且
是左焦点且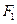 到直线
到直线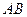 的距离
的距离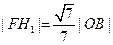 ,求椭圆的离心率.
,求椭圆的离心率.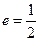
由△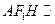 △
△ 得,
得,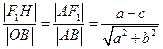 ,
,
所以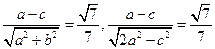 ,
,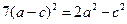 ,
,
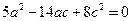 ,得
,得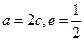 .
.
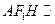 △
△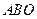 得,
得,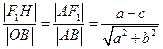 ,
,所以
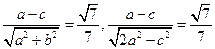 ,
,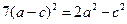 ,
,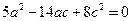 ,得
,得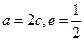 .
.
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
题目内容
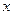 轴上的椭圆与
轴上的椭圆与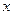 轴的负半轴交于点
轴的负半轴交于点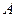 ,与
,与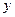 轴的正半轴交于点
轴的正半轴交于点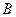 ,
,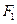 是左焦点且
是左焦点且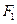 到直线
到直线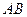 的距离
的距离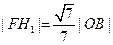 ,求椭圆的离心率.
,求椭圆的离心率.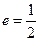
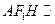 △
△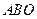 得,
得,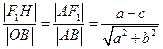 ,
,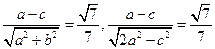 ,
,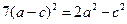 ,
,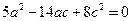 ,得
,得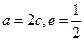 .
.
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案