题目内容
(本小题满分12分)
设椭圆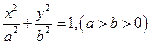 的左右焦点分别为
的左右焦点分别为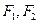 ,离心率
,离心率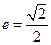 ,右准线为
,右准线为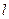 ,
,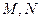 是
是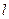 上的两个动点,
上的两个动点,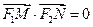 。
。
(Ⅰ)若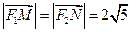 ,求
,求 的值;
的值;
(Ⅱ)证明:当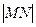 取最小值时,
取最小值时,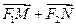 与
与 共线。
共线。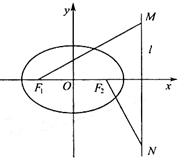
设椭圆
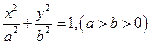 的左右焦点分别为
的左右焦点分别为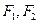 ,离心率
,离心率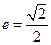 ,右准线为
,右准线为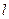 ,
,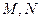 是
是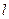 上的两个动点,
上的两个动点,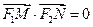 。
。(Ⅰ)若
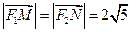 ,求
,求 的值;
的值;(Ⅱ)证明:当
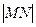 取最小值时,
取最小值时,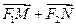 与
与 共线。
共线。
(Ⅰ)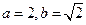
(Ⅱ)证明见解析。
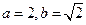
(Ⅱ)证明见解析。
由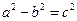 与
与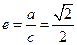 ,得
,得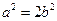 ,
,
 ,
, 的方程为
的方程为 。
。
设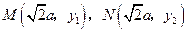 ,
,
则 ,
,
由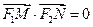 得
得
 。 ①
。 ①
(Ⅰ)由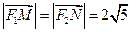 ,得
,得
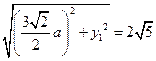 , ②
, ②
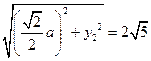 , ③
, ③
由①、②、③三式,消去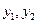 ,并求得
,并求得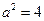 ,
,
故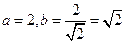 。
。
(Ⅱ)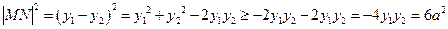 ,
,
当且仅当 或
或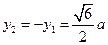 时,
时,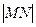 取最小值
取最小值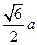 ,
,
此时, ,
,
故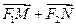 与
与 共线。
共线。
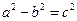 与
与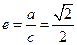 ,得
,得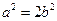 ,
, ,
,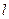 的方程为
的方程为 。
。设
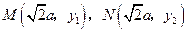 ,
,则
 ,
,由
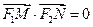 得
得 。 ①
。 ①(Ⅰ)由
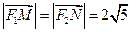 ,得
,得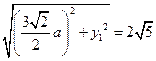 , ②
, ②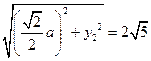 , ③
, ③由①、②、③三式,消去
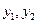 ,并求得
,并求得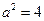 ,
,故
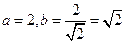 。
。(Ⅱ)
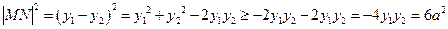 ,
,当且仅当
 或
或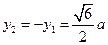 时,
时,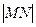 取最小值
取最小值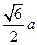 ,
,此时,
 ,
,故
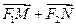 与
与 共线。
共线。
练习册系列答案
相关题目
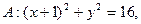 圆心为A,动圆M过点B(1,0)且和圆A相切,动圆的圆心M的轨迹记为C.
圆心为A,动圆M过点B(1,0)且和圆A相切,动圆的圆心M的轨迹记为C.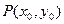 为曲线C上一点,求证:直线
为曲线C上一点,求证:直线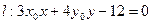 与曲线C有且只有一个交点.
与曲线C有且只有一个交点.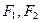 为椭圆的左右焦点,抛物线以
为椭圆的左右焦点,抛物线以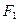 为顶点,
为顶点,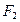 为焦点,设
为焦点,设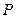 为椭圆与抛物线的一个交点,椭圆离心率为
为椭圆与抛物线的一个交点,椭圆离心率为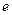 ,且
,且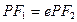 ,求
,求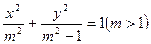 上一点P到其左焦点的距离为3,到右焦点的距离为1,则P点到右准线的距离为
上一点P到其左焦点的距离为3,到右焦点的距离为1,则P点到右准线的距离为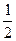
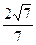
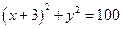 ,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足
,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足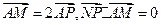 ,点N的轨迹为曲线E。
,点N的轨迹为曲线E。
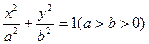 的焦点为F1(0,c)、F2(0,一c)(c>0),抛物线
的焦点为F1(0,c)、F2(0,一c)(c>0),抛物线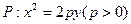 的焦点与F1重合,过F2的直线l与抛物线P相切,切点在第一象限,且与椭圆C相交于A、B两点,且
的焦点与F1重合,过F2的直线l与抛物线P相切,切点在第一象限,且与椭圆C相交于A、B两点,且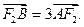
 ,求抛物线P的方程;
,求抛物线P的方程; 时,求椭圆离心率e的取值范围。
时,求椭圆离心率e的取值范围。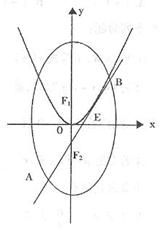
 与直线
与直线 交于
交于 ,
, 两点,过原点与线段
两点,过原点与线段 中点的直线的斜率为
中点的直线的斜率为 ,则
,则 ( )
( )


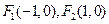 是椭圆的两个焦点,过
是椭圆的两个焦点,过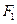 的直线
的直线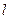 交椭圆于
交椭圆于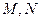 ,若
,若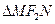 的周长为
的周长为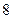 ,则椭圆方程为( ).
,则椭圆方程为( ).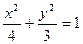
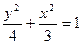
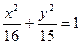
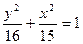
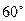 的菱形的四个顶点,则椭圆的离心率为 .
的菱形的四个顶点,则椭圆的离心率为 .