题目内容
3.(1-x)10的展开式中x3的系数为( )| A. | -120 | B. | 120 | C. | -45 | D. | 45 |
分析 在二项展开式的通项公式中,令x的幂指数等于3,求出r的值,即可求得展开式中x3的系数.
解答 解:(1-x)10的展开式的通项公式为 Tr+1=${C}_{10}^{r}$•(-x)r,令r=3,可得展开式中x3的系数为-${C}_{10}^{3}$=-120,
故选:A.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题.

练习册系列答案
相关题目
13.下列函数的最小值为2的是 ( )
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$(0<x<$\frac{π}{2}$) | ||
| C. | y=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$ | D. | y=tanx+$\frac{1}{tanx}$(0<x<$\frac{π}{2}$) |
15.已知集合A={y|y=x2+2x-3},$B=\left\{{\left.y\right|y=x+\frac{1}{x},x>0}\right\}$,则有( )
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=φ |
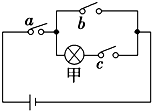 如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$.
如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$. 如图,在等腰梯形ABCD中,AB∥CD,延长AB到点E,使∠BEC=∠CAD.若AC=$\sqrt{2}$,CD=CE=1,则BC=$\frac{\sqrt{2}}{2}$.
如图,在等腰梯形ABCD中,AB∥CD,延长AB到点E,使∠BEC=∠CAD.若AC=$\sqrt{2}$,CD=CE=1,则BC=$\frac{\sqrt{2}}{2}$.