题目内容

12．一张储蓄卡的密码共有8位数字，每位数字都可从0～9中任选一个．某人在银行自动提款机上取钱时，忘记了密码的最后一位数字，求：
（1）任意按最后一位数字，不超过2次就按对的概率：
（2）如果他记得密码的最后一位是偶数，不超过2次就按对的概率．

分析 （1）任意按最后一位数字，不超过2次就按对的有两种情形一种是按1次就按对了和第一次没有按对，第二次按对了，求两种情形的概率和即可；
（2）在记得最后一位是偶数的前提下不超过2次就按对，利用条件概率的公式进行求解即可．

解答 解：记“第i次按对密码”为事件Ai（i=1，2）“不超过2次就按对密码“为事件A
（1）P（A）=P（A1）+P（$\overline{{A}_{1}}$A2）=$\frac{1}{10}$+$\frac{9}{10}×\frac{1}{9}$=$\frac{1}{5}$
（2）记“最后一位按偶数”为事件B
则P（A|B）=P（A1|B）+P（（$\overline{{A}_{1}}$A2|B）=$\frac{1}{5}$+$\frac{4}{5}×\frac{1}{4}$=$\frac{2}{5}$．

点评 本题主要考查了等可能事件的概率，解题的关键就是理解不超过2次就按对，属于中档题．

练习册系列答案
相关题目
2．某同学为了解秋冬季节用电量（y度）与气温（x℃）的关系，由下表数据计算出回归直线方程为y=-2x+60，则表中a的值为（　　）
气温181310-1
用电量（度）2434a64
A．40B．39C．38D．37
3．（1-x）10的展开式中x3的系数为（　　）
A．-120B．120C．-45D．45
20．如果对任意一个三角形，只要它的三边a，b，c都在函数f（x）的定义域内，就有f（a），f（b），f（c）也是某个三角形的三边长，则称f（x）为“和美型函数”．现有下列函数：①f（x）=$\sqrt{x}$；  ②g（x）=sinx，x∈（0，π）；  ③φ（x）=2x；④h（x）=lnx，x∈[2，+∞）．其中是“和美型函数”的函数序号为①④．（写出所有正确的序号）
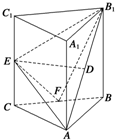7．三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC，△ABC为等腰直角三角形，∠BAC=90°且AB=AA1，D，E，F分别是B1A，CC1，BC的中点．
（1）求证：DE∥平面ABC；
（2）求证：B1F⊥平面AEF．
17．已知平面内n（n∈N+）条直线，任意两条都相交，任意三条不共点，这n条直线将平面分割成an个区域，则an=$\frac{{n}^{2}+n+2}{2}$．
4．已知集合A={0，1，2}，集合B={-1，0，1}，则集合A∩B=（　　）
A．{-1，0，1，2}B．{0，1}C．{-1，6}D．∅
1．（1）设实数x，y满足不等式组$\left\{\begin{array}{l}|{x+y-6}|≤2\\ y≤2x+4≤4y+4\end{array}\right.$，作出不等式组表示的平面区域，并求当a＞0时，z=y-ax的最大值；
（2）若关于x的不等式组$0≤{x^2}+\frac{7}{9}x-\frac{2^n}{{{{（{{2^n}+1}）}^2}}}≤\frac{2}{9}$对任意n∈N*恒成立，求所有这样的解x构成的集合．
2．若A（-1，1），B（1，3），C（x，5），且$\overrightarrow{AB}$=$λ\overrightarrow{BC}$，则实数λ等于（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网