题目内容
(本题满分12分),
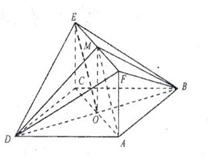
如图,菱形ABCD所在平面与矩形ACEF所在平面互相垂直,已知BD=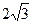 AF,且点M是线段EF的中点.
AF,且点M是线段EF的中点.
(1)求证:AM∥平面BDE;
(2)求平面DEF与平面BEF所成的角.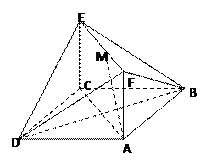
如图,菱形ABCD所在平面与矩形ACEF所在平面互相垂直,已知BD=
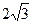 AF,且点M是线段EF的中点.
AF,且点M是线段EF的中点.(1)求证:AM∥平面BDE;
(2)求平面DEF与平面BEF所成的角.
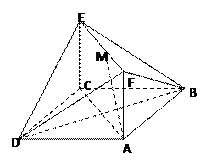
(1)略(2)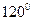
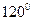
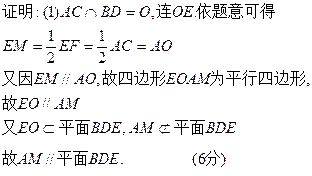


练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
题目内容
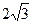 AF,且点M是线段EF的中点.
AF,且点M是线段EF的中点.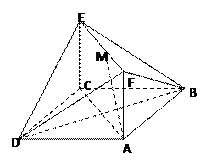
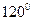
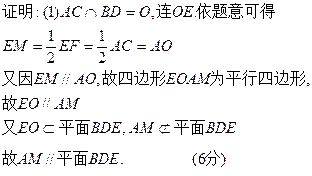



 华东师大版一课一练系列答案
华东师大版一课一练系列答案