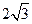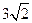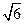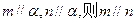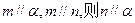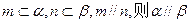题目内容
(本题共12分)如图,在四棱锥P-ABCD中,底面ABCD为菱形, 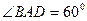 ,Q为AD的中点
,Q为AD的中点
(1) 若PA=PD,求证: 平面PQB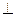 平面PAD
平面PAD
(2)点M在线段PC上,PM=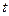 PC,试确定实数
PC,试确定实数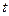 的值,使得PA//平面MQB
的值,使得PA//平面MQB
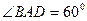 ,Q为AD的中点
,Q为AD的中点(1) 若PA=PD,求证: 平面PQB
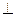 平面PAD
平面PAD(2)点M在线段PC上,PM=
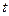 PC,试确定实数
PC,试确定实数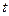 的值,使得PA//平面MQB
的值,使得PA//平面MQB
(1)略
(2)可知当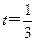 时, PA//平面MQB
时, PA//平面MQB
(2)可知当
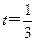 时, PA//平面MQB
时, PA//平面MQB解(1)依题意,可设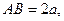 故
故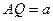 又
又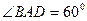
由余弦定理可知
 =3
=3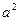
∴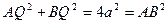
故可知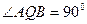 ,可知
,可知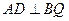 ,………………………………………2分
,………………………………………2分
(另解:连结BD,由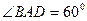 ,AD=AB,可知
,AD=AB,可知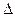 AB
AB D为等边三角形,又Q为AD的中点,所以也可证得
D为等边三角形,又Q为AD的中点,所以也可证得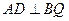 )
)
又在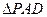

 中,PA="PD" ,Q为AD的中点
中,PA="PD" ,Q为AD的中点
∴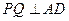 , …………………………………………………………………………3分
, …………………………………………………………………………3分
又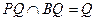
∴
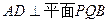 ………………………………………………………………4分
………………………………………………………………4分
又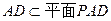 所以平面PQB
所以平面PQB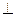 平面PAD………………………………6分
平面PAD………………………………6分
(2)连结AC交BQ于点O ,连结MO,
欲使 PA//平面MQB
只需 满足 PA//OM 即可………………………………………………………….7分
又由已知 AQ//BC
易证得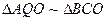 ∴
∴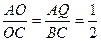 …
… …………………………………8分
…………………………………8分
故只需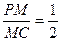 ,即
,即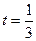 时,满足题意…………………………………………10分
时,满足题意…………………………………………10分
∵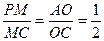
∴可知 PA//OM 又

所以可知当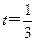 时, PA//平面MQB……………………………………………...12分
时, PA//平面MQB……………………………………………...12分
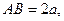 故
故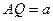 又
又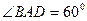
由余弦定理可知
 =3
=3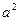
∴
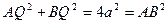
故可知
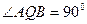 ,可知
,可知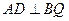 ,………………………………………2分
,………………………………………2分(另解:连结BD,由
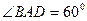 ,AD=AB,可知
,AD=AB,可知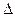 AB
AB D为等边三角形,又Q为AD的中点,所以也可证得
D为等边三角形,又Q为AD的中点,所以也可证得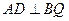 )
)又在
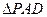

 中,PA="PD" ,Q为AD的中点
中,PA="PD" ,Q为AD的中点∴
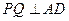 , …………………………………………………………………………3分
, …………………………………………………………………………3分又
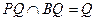
∴

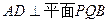 ………………………………………………………………4分
………………………………………………………………4分又
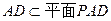 所以平面PQB
所以平面PQB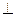 平面PAD………………………………6分
平面PAD………………………………6分(2)连结AC交BQ于点O ,连结MO,
欲使 PA//平面MQB
只需 满足 PA//OM 即可………………………………………………………….7分
又由已知 AQ//BC
易证得
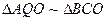 ∴
∴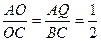 …
… …………………………………8分
…………………………………8分故只需
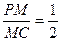 ,即
,即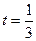 时,满足题意…………………………………………10分
时,满足题意…………………………………………10分∵
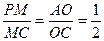
∴可知 PA//OM 又


所以可知当
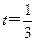 时, PA//平面MQB……………………………………………...12分
时, PA//平面MQB……………………………………………...12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
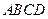 为矩形,
为矩形,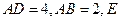 、
、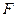 分别是线段
分别是线段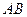 、
、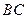 的中点,
的中点,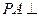 平面
平面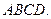 (1)求证:
(1)求证: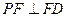 ;
;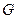 在
在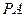 上,且
上,且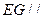 平面
平面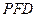 ,试确定点
,试确定点 ,
, 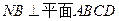 ,且MD=NB=1,E为BC 的中点 (1)求异面直线NE与AM所成角的余弦值
,且MD=NB=1,E为BC 的中点 (1)求异面直线NE与AM所成角的余弦值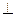 平面AMN,并求线段AS的长;
平面AMN,并求线段AS的长;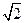 .
.
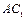 中,
中, 为棱
为棱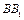 的中点,则在平面
的中点,则在平面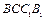 内过点
内过点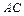 成
成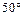 角的直线有( )
角的直线有( )
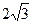 AF,且点M是线段EF的中点.
AF,且点M是线段EF的中点.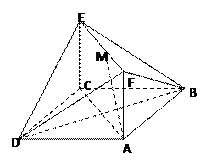
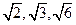 ,则对角线长为( )
,则对角线长为( )