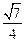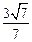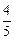题目内容
(本小题满分12分)
如图:在四棱锥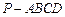 中,底面
中,底面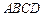 是菱形,
是菱形,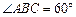 ,
,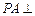 平面
平面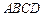 ,
,
点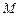 、
、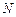 分别为
分别为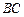 、
、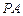 的中点,
的中点,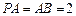 .
.
(I)证明: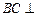 平面
平面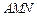 ;
;
(II)在线段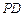 上是否存在一点
上是否存在一点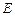 ,使得
,使得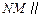 平面
平面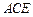 ;若存在,
;若存在, 求出
求出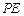 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
如图:在四棱锥
 中,底面
中,底面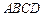 是菱形,
是菱形, ,
, 平面
平面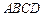 ,
,点
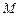 、
、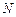 分别为
分别为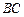 、
、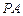 的中点,
的中点,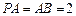 .
.(I)证明:
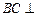 平面
平面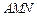 ;
;(II)在线段
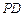 上是否存在一点
上是否存在一点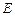 ,使得
,使得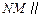 平面
平面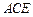 ;若存在,
;若存在, 求出
求出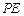 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
(I)略
(II)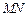
 平面
平面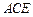 ,即在
,即在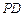 上存在一点
上存在一点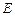 ,使得
,使得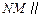 平面
平面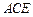 ,
,
此时 .
.
(II)
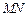
 平面
平面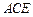 ,即在
,即在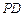 上存在一点
上存在一点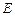 ,使得
,使得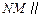 平面
平面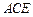 ,
, 此时
 .
.解:(Ⅰ)因为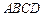 为菱形,所以
为菱形,所以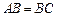
又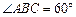 ,所以
,所以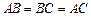 ,
,
又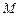 为
为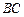 中点,所以
中点,所以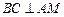
而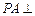 平面
平面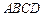 ,
,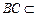 平面
平面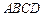 ,所以
,所以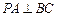
又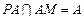 ,所以
,所以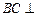 平面
平面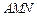 (6分)
(6分)
(II)存在
取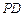 中点
中点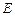 ,连结
,连结 ,
,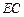 ,
,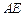 ,(8分)
,(8分)
因为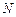 ,
,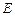 分别为
分别为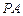 、
、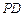 中点,所以
中点,所以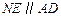 且
且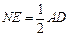
又在菱形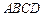 中,
中,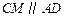 ,
,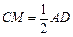
所以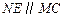 ,
, ,即
,即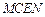 是平行四边形
是平行四边形
所以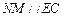 ,又
,又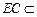 平面
平面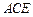 ,
,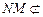 平面
平面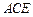
所以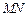
 平面
平面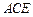 ,即在
,即在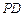 上存在一点
上存在一点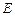 ,使得
,使得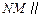 平面
平面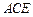 ,(10分)
,(10分)
此时 .(12分)
.(12分)
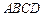 为菱形,所以
为菱形,所以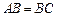
又
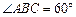 ,所以
,所以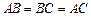 ,
,又
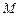 为
为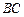 中点,所以
中点,所以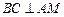
而
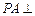 平面
平面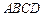 ,
,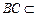 平面
平面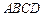 ,所以
,所以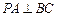
又
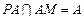 ,所以
,所以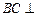 平面
平面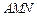 (6分)
(6分)(II)存在
取
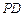 中点
中点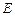 ,连结
,连结 ,
,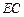 ,
,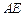 ,(8分)
,(8分)因为
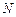 ,
,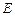 分别为
分别为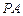 、
、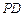 中点,所以
中点,所以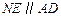 且
且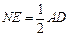
又在菱形
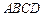 中,
中,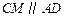 ,
,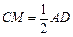
所以
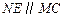 ,
, ,即
,即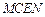 是平行四边形
是平行四边形所以
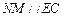 ,又
,又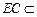 平面
平面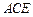 ,
,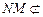 平面
平面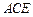
所以
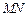
 平面
平面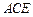 ,即在
,即在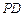 上存在一点
上存在一点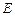 ,使得
,使得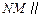 平面
平面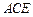 ,(10分)
,(10分)此时
 .(12分)
.(12分)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的底面是正方形,每条侧棱长都是底面边长的
的底面是正方形,每条侧棱长都是底面边长的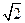 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。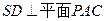 ,求二面角
,求二面角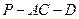 的大小;
的大小;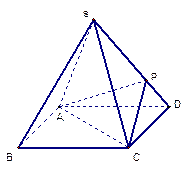
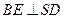 ,若存在,求
,若存在,求 的值;若不存在,试说明理由。
的值;若不存在,试说明理由。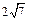 ,PB=10,F是线段PB上一点,
,PB=10,F是线段PB上一点,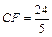 ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.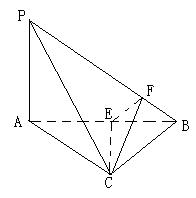
 为矩形,
为矩形,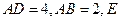 、
、 分别是线段
分别是线段 、
、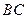 的中点,
的中点,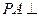 平面
平面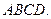 (1)求证:
(1)求证: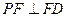 ;
;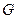 在
在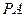 上,且
上,且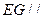 平面
平面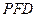 ,试确定点
,试确定点 ,
, 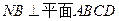 ,且MD=NB=1,E为BC 的中点 (1)求异面直线NE与AM所成角的余弦值
,且MD=NB=1,E为BC 的中点 (1)求异面直线NE与AM所成角的余弦值 平面AMN,并求线段AS的长;
平面AMN,并求线段AS的长; 中,
中, 分别是棱
分别是棱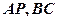 的中点,
的中点,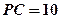 ,
,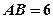 ,
,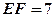 ,则异面直线
,则异面直线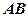 与
与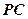 所成的角为 ( )
所成的角为 ( )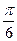
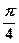


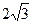 AF,且点M是线段EF的中点.
AF,且点M是线段EF的中点.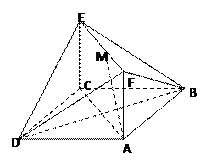
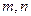 为两条不同的直线,
为两条不同的直线,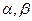 为两个不同的平面,给定下列条件:
为两个不同的平面,给定下列条件: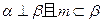 ;②
;②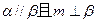 ;③
;③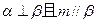 ;④
;④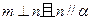 .其中可以判定
.其中可以判定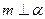 的有 ( )
的有 ( )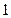 个
个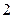 个
个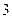 个
个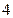 个
个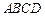 中,
中,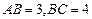 ,沿对角线
,沿对角线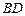 将
将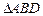 折起到
折起到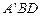 的位置,且
的位置,且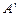 在平面
在平面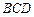 内的射影
内的射影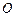 落在
落在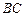 边上,则二面角
边上,则二面角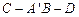 的平面角的正弦值为( )
的平面角的正弦值为( )