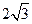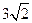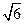题目内容
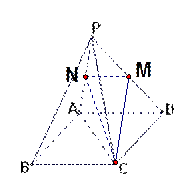
(本小题满分12分)已知四棱锥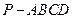 的底面是边长为2的菱形,且
的底面是边长为2的菱形,且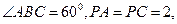
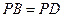 .
.
(Ⅰ)若O是AC与BD的交点,求证: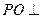 平面
平面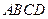 ;
;
(Ⅱ)若点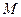 是
是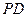 的中点,求异面直线
的中点,求异面直线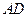 与
与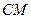 所成角的余弦值.
所成角的余弦值.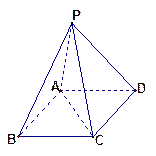
 的底面是边长为2的菱形,且
的底面是边长为2的菱形,且
 .
.(Ⅰ)若O是AC与BD的交点,求证:
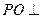 平面
平面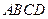 ;
;(Ⅱ)若点
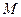 是
是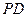 的中点,求异面直线
的中点,求异面直线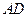 与
与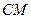 所成角的余弦值.
所成角的余弦值.
(Ⅰ)证明略;
(Ⅱ)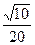
(Ⅱ)
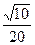
(Ⅰ)连接AC与BD交于点O,连OP.
∵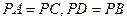 ,且O是AC和BD的中点,
,且O是AC和BD的中点,
∴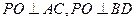
∴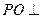 平面
平面 .
.
(Ⅱ)取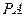 的中点
的中点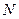 ,连接
,连接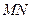 ,则
,则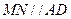 ,则
,则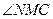 就是所求的角,根据题意得
就是所求的角,根据题意得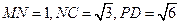
所以,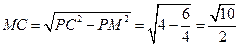
故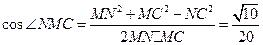

∵
 ,且O是AC和BD的中点,
,且O是AC和BD的中点,∴
∴
 平面
平面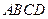 .
.(Ⅱ)取
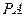 的中点
的中点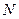 ,连接
,连接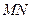 ,则
,则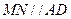 ,则
,则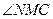 就是所求的角,根据题意得
就是所求的角,根据题意得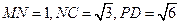
所以,
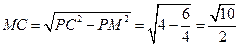
故
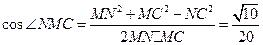



练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 的正方体ABCD—A1B1C1D1中,E、F、H分别是棱BB1、CC1、DD1的中点。
的正方体ABCD—A1B1C1D1中,E、F、H分别是棱BB1、CC1、DD1的中点。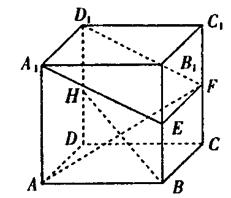
 的正方体
的正方体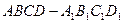 中,
中,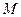 是
是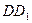 的中点,
的中点,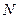 在线段
在线段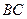 上,且
上,且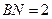 .
.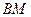 与
与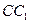 所成角的余弦值;
所成角的余弦值;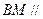 面
面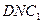 ;
;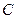 到面
到面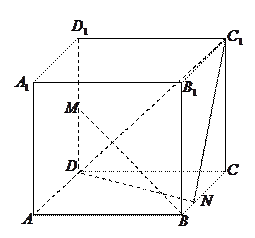
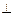 平面PAD;
平面PAD;
 .
.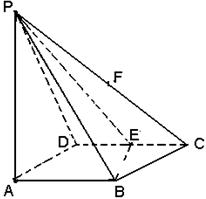
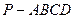 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱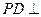 底面ABCD,
底面ABCD,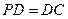 ,E是PC的中点.
,E是PC的中点.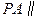 平面
平面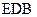 ;
;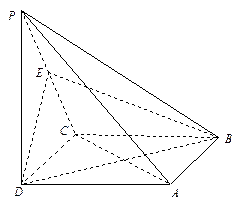
 中,
中, 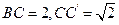 .
.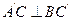 ;
;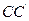 上确定一点P,使直线
上确定一点P,使直线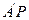 与平面
与平面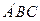 所成角的正弦等于
所成角的正弦等于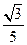 .
.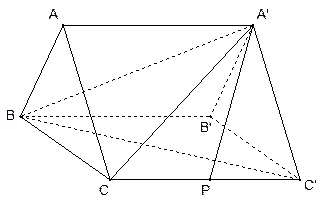
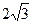 AF,且点M是线段EF的中点.
AF,且点M是线段EF的中点.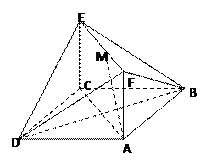
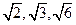 ,则对角线长为( )
,则对角线长为( )