题目内容
18.已知数列{an}满足4an=an-1-3(n≥2)且n∈N*,且a1=-$\frac{3}{4}$,设bn+2=3log${\;}_{\frac{1}{4}}$(an+1)(n∈N*),数列{cn}满足cn=(an+1)bn.(Ⅰ)求证{an+1}是等比数列并求出数列{an}的通项公式;
(Ⅱ)求数列{cn}的前n项和Sn;
(Ⅲ)对于任意n∈N*,t∈[0,1],cn≤tm2-m-$\frac{1}{2}$恒成立,求实数m的取值范围.
分析 (Ⅰ)运用等比数列的定义可得{an+1}是等比数列,其中首项是a1+1=$\frac{1}{4}$,公比为$\frac{1}{4}$,再由等比数列的通项公式,即可得到所求;
(Ⅱ)运用对数的性质,可得数列{bn}的通项,由错位相减法,即可得到前n项和Sn;
(Ⅲ)运用作差法,可得数列{cn}的单调性,即有cn的最大值,再由恒成立思想及异常函数的性质,即可得到m的范围.
解答 解:(Ⅰ)证明:由4an=an-1-3,
则4an+4=an-1+1,即(an+1)=$\frac{1}{4}$(an-1+1),
∴{an+1}是等比数列,其中首项是a1+1=$\frac{1}{4}$,公比为$\frac{1}{4}$,
∴an+1=($\frac{1}{4}$)n,即有an=($\frac{1}{4}$)n-1;
(Ⅱ)bn+2=3log${\;}_{\frac{1}{4}}$${\;}^{{(a}_{n}+1)}$(n∈N*),
则bn=3n-2,
由(Ⅰ)知,an+1=($\frac{1}{4}$)n,bn=3n-2,
则cn=(3n-2)•($\frac{1}{4}$)n,
前n项和Sn=1•$\frac{1}{4}$+4•($\frac{1}{4}$)2+7•($\frac{1}{4}$)3+…+(3n-5)•($\frac{1}{4}$)n-1+(3n-2)•($\frac{1}{4}$)n,
$\frac{1}{4}$Sn=1•($\frac{1}{4}$)2+4•($\frac{1}{4}$)3+7•($\frac{1}{4}$)4+…+(3n-5)•($\frac{1}{4}$)n+(3n-2)•($\frac{1}{4}$)n+1,
两式相减得$\frac{3}{4}$Sn=$\frac{1}{4}$+3[($\frac{1}{4}$)2+($\frac{1}{4}$)3+…($\frac{1}{4}$)n]-(3n-2)•($\frac{1}{4}$)n+1
=$\frac{1}{4}$+3•$\frac{\frac{1}{16}(1-\frac{1}{{4}^{n-1}})}{1-\frac{1}{4}}$]-(3n-2)•($\frac{1}{4}$)n+1
=$\frac{1}{2}$-(3n+2)•($\frac{1}{4}$)n+1
即有Sn=$\frac{2}{3}$-$\frac{3n+2}{3}$•($\frac{1}{4}$)n;
(Ⅲ)cn+1-cn=(3n+1)•($\frac{1}{4}$)n+1-(3n-2)•($\frac{1}{4}$)n
=9(1-n)•($\frac{1}{4}$)n+1;
∴当n=1时,c2=c1=$\frac{1}{4}$,
当n≥2时,cn+1<cn,即c1=c2>c3>c4>…>cn,
∴当n=1或n=2时,cn取最大值是$\frac{1}{4}$,
只须$\frac{1}{4}$≤tm2-m-$\frac{1}{2}$,即tm2-m-$\frac{3}{4}$≥0对于任意t∈[0,1]恒成立,
即$\left\{\begin{array}{l}{{m}^{2}-m-\frac{3}{4}≥0}\\{m+\frac{3}{4}≤0}\end{array}\right.$即为$\left\{\begin{array}{l}{m≥\frac{3}{2}或m≤-\frac{1}{2}}\\{m≤-\frac{3}{4}}\end{array}\right.$,
则m≤-$\frac{3}{4}$.
点评 本题考查等差数列和等比数列的通项和求和公式的运用,考查数列的求和方法:错位相减法,以及数列的单调性的运用:求最值,属于中档题.

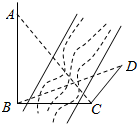 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)| A. | 10$\sqrt{2}$ | B. | 10$\sqrt{6}$ | C. | 10$\sqrt{3}$ | D. | 10 |
| A. | 120 | B. | 210 | C. | 252 | D. | 45 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{12}$ |
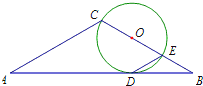 如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.
如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.