题目内容
3.($\sqrt{x}$+$\frac{1}{\root{3}{x}}$)2n(n∈N*)展开式中只有第6项系数最大,则其常数项为( )| A. | 120 | B. | 210 | C. | 252 | D. | 45 |
分析 由已知得到展开式的通项,得到第6项系数,根据二项展开式的系数性质得到n,可求常数项.
解答 解:由已知($\sqrt{x}$+$\frac{1}{\root{3}{x}}$)2n(n∈N*)展开式中只有第6项系数为${C}_{2n}^{5}$最大,
所以展开式有11项,所以2n=10,即n=5,
又展开式的通项为${C}_{10}^{k}(\sqrt{x})^{10-k}(\frac{1}{\root{3}{x}})^{k}$=${C}_{10}^{k}{x}^{5-\frac{5}{6}}k$,
令5-$\frac{5}{6}k$=0解得k=6,
所以展开式的常数项为${C}_{10}^{6}={C}_{10}^{4}$=210;
故选:B
点评 本题考查了二项展开式的系数以及求特征项;解得本题的关键是求出n,利用通项求特征项.

练习册系列答案
相关题目
14.某中学为了解初三年级学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下:
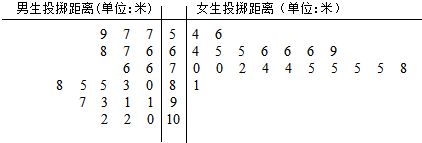
已知该项目评分标准为:
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,有6人的投掷距离低于7.0米,现从这6名男生中随机抽取2名男生,求抽取的2名男生得分都是4分的概率;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)

已知该项目评分标准为:
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
(Ⅱ)从上述20名男生中,有6人的投掷距离低于7.0米,现从这6名男生中随机抽取2名男生,求抽取的2名男生得分都是4分的概率;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)
11.已知函数f(x)=x2-x+7,求f′(4)=( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
9.已知函数f(x)=sin(ωx+$\frac{π}{3}$),ω>0,f($\frac{π}{6}$)=f($\frac{π}{3}$),f(x)在区间($\frac{π}{6}$,$\frac{π}{3}$)有最小值无最大值,则?的值为( )
| A. | $\frac{14}{3}$ | B. | $\frac{13}{3}$ | C. | $\frac{3}{14}$ | D. | $\frac{3}{13}$ |