ƒøƒ⁄»›
°æƒø°ø‘⁄µ˜≤ȃ–≈Æ≥ÀøÕ «∑Ò‘Œª˙µƒ«Èøˆ÷–£¨“—÷™ƒ–≥ÀøÕ‘Œª˙Œ™28»À£¨≤ªª·‘Œª˙µƒ“≤ «28»À£¨∂¯≈Æ≥ÀøÕ‘Œª˙Œ™28»À£¨≤ªª·‘Œª˙µƒŒ™56»À£¨![]() ∆‰÷–
∆‰÷– ![]() Œ™—˘±æ»›¡ø°£
Œ™—˘±æ»›¡ø°£
P(K2°›k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
£®1£©∏˘æ›“‘…œ ˝æ›Ω®¡¢“ª∏ˆ ![]() µƒ¡–¡™±Ì£ª
µƒ¡–¡™±Ì£ª
£®2£© ‘≈–∂œ «∑Ò”–95£•µƒ∞—Œ’»œŒ™ «∑Ò‘Œª˙”Ζ‘±”–πÿ£ø
°æ¥∞∏°ø
£®1£©
Ω‚£∫2°¡2¡–¡™±Ì»Áœ¬£∫
‘Œª˙ | ≤ª‘Œª˙ | ∫œº∆ | |
ƒ–≥ÀøÕ | 28 | 28 | 56 |
≈Æ≥ÀøÕ | 28 | 56 | 84 |
∫œº∆ | 56 | 84 | 140 |
£®2£©
Ω‚£∫ºŸ…Ë «∑Ò‘Œª˙”Ζ‘±Œfiπÿ£¨‘Ú
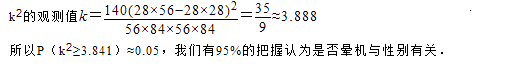
°æΩ‚Œˆ°ø±æÂ÷˜“™øº≤È¡À∂¿¡¢–‘ºÏ—ȵƒ”¶”√£¨Ω‚戌 µƒπÿº¸ «£®1£©∏˘æ›ƒ–≥ÀøÕ‘Œª˙Œ™28»À£¨≤ªª·‘Œª˙µƒ“≤ «28»À£¨∂¯≈Æ≥ÀøÕ‘Œª˙Œ™28»À£¨≤ªª·‘Œª˙µƒŒ™56»À£¨ª≠≥ˆ¡–¡™±Ì£ª£®2£©∏˘æ›π´ Ω£¨«Û≥ˆ’‚◊È ˝æ›µƒπ€≤‚÷µ£¨∞—π€≤‚÷µÕ¨¡ŸΩÁ÷µΩ¯––±»Ωœ£¨º¥ø…µ√µΩΩ·¬€..

¡∑œ∞≤·œµ¡–¥∞∏
œ‡πÿƒø