题目内容
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图). 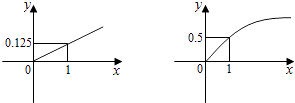
(1)分别写出两种产品的收益和投资的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大的收益,其最大收益为多少万元?
【答案】
(1)解:设f(x)=k1x,g(x)=k2 ![]() ,
,
由题意,可得f(1)=0.125=k1,g(1)=k2=0.5,
则f(x)=0.125x(x≥0),g(x)=0.5 ![]() (x≥0)
(x≥0)
(2)解:设投资债券类产品x万元,则股票类投资为(20﹣x)万元,
由题意,得y=f(x)+g(20﹣x)=0.125x+0.5 ![]() (0≤x≤20),
(0≤x≤20),
令t= ![]() ,则有x=20﹣t2,
,则有x=20﹣t2,
∴y=0.125(20﹣t2)+0.5t=﹣0.125(t﹣2)2+3,
当t=2,即x=16万元时,收益最大,此时ymax=3万元,
则投资债券等稳健型产品16万元,投资股票等风险型产品4万元获得收益最大,最大收益为4万元
【解析】(1)利用待定系数法确定出f(x)与g(x)解析式即可;(2)设设投资债券类产品x万元,则股票类投资为(20﹣x)万元,根据y=f(x)+g(x)列出二次函数解析式,利用二次函数的性质判断即可得到结果.

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案【题目】在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,![]() 其中
其中 ![]() 为样本容量。
为样本容量。
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)根据以上数据建立一个 ![]() 的列联表;
的列联表;
(2)试判断是否有95%的把握认为是否晕机与性别有关?