题目内容
【题目】(Ⅰ)设f(x)= 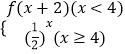 ,求f(1+log23)的值;
,求f(1+log23)的值;
(Ⅱ)已知g(x)=ln[(m2﹣1)x2﹣(1﹣m)x+1]的定义域为R,求实数m的取值范围.
【答案】解:(Ⅰ)∵1+log23∈(2,3),
∴ ![]() ;
;
(Ⅱ)由题设得:(m2﹣1)x2﹣(1﹣m)x+1>0(*)在x∈R时恒成立,
若m2﹣1=0m=±1,
当m=1时,(*)式可化为:1>0恒成立,
当m=﹣1时,(*)式可化为:﹣2x+1>0不恒成立,
∴m=1;
若m2﹣1≠0,
则 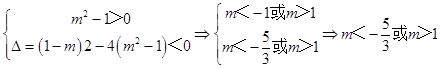
综上,实数m的取值范围是 ![]()
【解析】(I)由1+log23∈(2,3),故f(1+log23)=f(3+log23),进而根据指数的运算性质,可得答案.(II)若g(x)=ln[(m2﹣1)x2﹣(1﹣m)x+1]的定义域为R,则(m2﹣1)x2﹣(1﹣m)x+1>0(*)在x∈R时恒成立,分m2﹣1=0和m2﹣1≠0两种情况结合二次函数的图象和性质,可得满足条件的实数m的取值范围.

【题目】分类变量X和Y的列联表如下:
y1 | y2 | 总计 | |
x1 | a | b | a+b |
x2 | c | d | c+d |
总计 | a+c | b+d | a+b+c+d |
则下列说法中正确的是( )
A.ad-bc越小,说明X与Y关系越弱
B.ad-bc越大,说明X与Y关系越强
C.(ad-bc)2越大,说明X与Y关系越强
D.(ad-bc)2越接近于0,说明X与Y关系越强
【题目】在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,![]() 其中
其中 ![]() 为样本容量。
为样本容量。
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)根据以上数据建立一个 ![]() 的列联表;
的列联表;
(2)试判断是否有95%的把握认为是否晕机与性别有关?
【题目】下表是一位母亲给儿子作的成长记录:
年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/cm | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
根据以上样本数据,她建立了身高 ![]() (cm)与年龄x(周岁)的线性回归方程为
(cm)与年龄x(周岁)的线性回归方程为 ![]() ,给出下列结论:
,给出下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本的中心点(42,117.1);
③儿子10岁时的身高是 ![]() cm;
cm;
④儿子年龄增加1周岁,身高约增加 ![]() cm.
cm.
其中,正确结论的个数是
A.1
B.2
C.3
D.4
