题目内容
【题目】已知函数![]() 在
在![]() 处有极值10.
处有极值10.
(1)求实数![]() 的值;
的值;
(2)设![]() ,讨论函数
,讨论函数![]() 在区间
在区间![]() 上的单调性.
上的单调性.
【答案】(1) ![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)根据题意得到关于m的方程组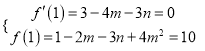 ,解方程组求得
,解方程组求得![]() 即可;(2)先判断函数
即可;(2)先判断函数![]() 的单调性,然后根据
的单调性,然后根据![]() 的取值情况分类讨论判断函数
的取值情况分类讨论判断函数![]() 在区间
在区间![]() 上的单调性。
上的单调性。
试题解析:
(1)![]() 定义域为
定义域为![]() ,
,
∵![]() 在
在![]() 处有极值10,
处有极值10,
∴![]() 且
且![]() ,
,
即![]() ,
,
解得: 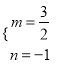 或
或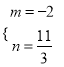 ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 处有极值10时,
处有极值10时, ![]() .
.
(2)由(1)可知![]() ,
,
∴![]()
当![]() 变化时,
变化时, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| 增 | 极大 | 减 | 极小 | 增 |
∴①当![]() ,即
,即![]() 时,
时, ![]() 在区间
在区间![]() 上的单调递增;
上的单调递增;
②当![]() ,即
,即![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;
上单调递减;
③当![]() 且
且![]() ,即
,即![]() 时,
时, ![]() 在区间
在区间![]() 上单调递减;
上单调递减;
④当![]() ,即
,即![]() 时,
时, ![]() 在区间
在区间![]() 上的单调递减,在区间
上的单调递减,在区间![]() 上单调递增;
上单调递增;
⑤当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增.
上单调递增.
综上所述:
当![]() 或
或![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在区间上
在区间上![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
【题目】在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,![]() 其中
其中 ![]() 为样本容量。
为样本容量。
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)根据以上数据建立一个 ![]() 的列联表;
的列联表;
(2)试判断是否有95%的把握认为是否晕机与性别有关?